Плотность вероятности двумерной случайной величины.

Как известно, случайная величина имеет плотность вероятности, если она непрерывна. Говоря о случайных величинах, двумерная случайная величина называется непрерывной, если ее функция распределения является непрерывной функцией. И существует вторая смешанная производная F ''xy (x,y), которая и является плотностью вероятности двумерной случайной величины.

Т.е. плотность вероятности это вторая смешанная производная от функции распределения двумерной случайной величины:

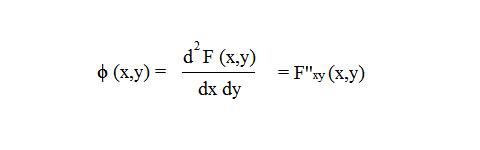
В общем виде плотность вероятности двумерной случайной величины выражается следующей формулой:

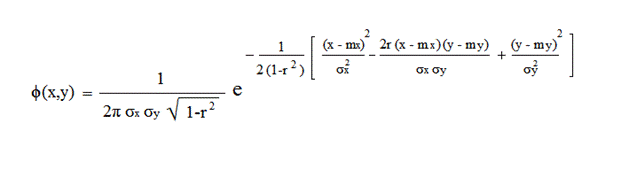
где

r - коэффициент корреляции случайных величин X и Y
σx - среднее квадратическое отклонение случайной величины X
σy - среднее квадратическое отклонение случайной величины Y
mx- математическое ожидание случайной величины X
my - математическое ожидание случайной величины Y

Если случайные величины подчинены нормальному закону распределения и не коррелированы (r = 0 ), то формула плотности вероятности примет вид:

Геометрический смысл вероятности двумерной случайной величины - это поверхность похожая на купол. На рис.3 изображен график плотности вероятности с параметрами r, σx, σy, mx, my, которые имеют следующие значения:

r = 0
σx = 2
σy = 2
mx = -1
my = 1

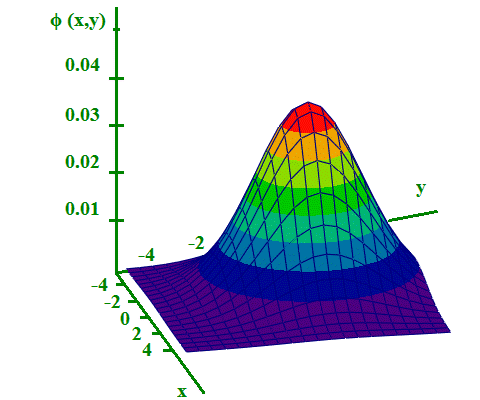
Рис.3

Рассматривая выражения для плотности вероятности двумерной случайной величины, можно заметить, что данный закон распределения задается пятью параметрами: двух координат центра распределения случайных величин x и y по осям X и Y, средних квадратических отклонений σx и σy, и коэффициентом корреляции случайных величин x и y.

Вероятность попадания непрерывной двумерной случайной величины в область D равна:

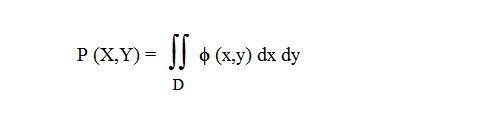
Функция распределения непрерывной двумерной случайной величины имеет вид:

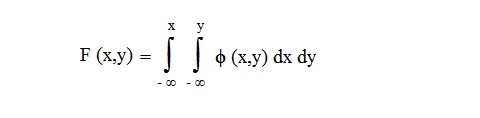
Билет № 9.