
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Существуют следующие типы шкал.
1. Номинальные. Это простейший тип измерения, в котором числа и символы используются только для классификации объектов. Факторы в данном случае выступают как ассоциативные показатели, обладающие информацией, которая может быть формализована в виде бинарных оценок двух уровней: 1(идентичен) или 0 (различен).
2. Порядковые шкалы. Используются в случаях, когда исследуемые объекты можно в результате сравнения расположить в определенной последовательности с учетом какого либо существенного фактора. Позволяют установит равноценность или доминирование. Использование порядковых шкал позволяет различать объекты и в тех случаях, когда фактор (критерий) не задан в явном виде, т.е. когда мы не знаем признака сравнения, но можем частично или полностью упорядочить объекты на основе системы предпочтений, которой обладает эксперт.
3. Интервальные шкалы. Используют для формализации оценок, полученных от экспертов. При использовании таких шкал для этих целей можно брать почти все статистические меры. Интервальная шкала – это порядковая + известные расстояния между двумя любыми числами на шкале (нулевая точка шкалы и единица измерения выбираются произвольно). Интервальные шкалы предполагают возможность трансформации оценок, полученных на одной шкале, в оценки на другой шкале при помощи уравнения х9=ах+b.
Разности между значениями на шкале интервалов становятся мерами на шкале отношений (обычной числовой шкале) по той простой причине, что в результате вычитания можно избавиться от постоянного слагаемого b.
4. Шкала отношений. Интервальная шкала + истинная нулевая точка. Отношение любых двух точек шкалы не зависит от единицы измерения.
В зависимости от существа или важности того или иного фактора на этапе подготовки и принятия решений могут быть использованы различные шкалы. Такие факторы, как затраты, прибыль, время, могут быть оценены по порядковой или интервальной шкале (в рублях, днях, условных единицах). Для оценки таких факторов, как срок окупаемости или сравнительная эффективность вариантов, может быть использована интервальная шкала; качественные или социальные факторы могут оцениваться по порядковым или номинальным шкалам.
Имитационное моделирование основано на воспроизведении с помощью ЭВМ развернутого во времени процесса функционирования системы с учетом взаимодействия с внешней средой. Основой всякой имитационной модели (ИМ) является:
· разработка модели исследуемой системы на основе частных имитационных моделей (модулей) подсистем, объединенных своими взаимодействиями в единое целое;
· выбор информативных (интегративных) характеристик объекта, способов их получения и анализа;
· построение модели воздействия внешней среды на систему в виде совокупности имитационных моделей внешних воздействующих факторов;
· выбор способа исследования имитационной модели в соответствии с методами планирования имитационных экспериментов (ИЭ).
Условно имитационную модель можно представить в виде действующих, программно (или аппаратно) реализованных блоков.
На рис. 3.1. показана структура имитационной модели. Блок имитации внешних воздействий (БИВВ) формирует реализации случайных или детерминированных процессов, имитирующих воздействия внешней среды на объект. Блок обработки результатов (БОР) предназначен для получения информативных характеристик исследуемого объекта. Необходимая для этого информация поступает из блока математической модели объекта (БМО). Блок управления (БУИМ) реализует способ исследования имитационной модели, основное его назначение – автоматизация процесса проведения ИЭ.
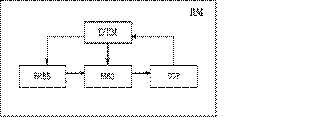
Рис. 3.1.
Целью имитационного моделирования является конструирование ИМ объекта и проведение ИЭ над ней для изучения закона функционирования и поведения с учетом заданных ограничений и целевых функций в условиях иммитации и взаимодействия с внешней средой.
К достоинствам метода имитационного моделирования могут быть отнесены:
o проведение ИЭ над ММ системы, для которой натурный эксперимент не осуществим по этическим соображениям или эксперимент связан с опасностью для жизни, или он дорог, или из-за того, что эксперимент нельзя провести с
o прошлым;
o решение задач, аналитические методы для которых неприменимы, например, в случае непрерывно- дискретных факторов, случайных воздействий, нелинейных характеристик элементов системы и т.п.;
o возможность анализа общесистемных ситуаций и принятия решения с помощью ЭВМ, в том числе для таких сложных систем, выбор критерия сравнения стратегий поведения которых на уровне проектирования не осуществим;
o сокращение сроков и поиск проектных решений, которые являются оптимальными по некоторым критериям оценка эффективности;
o проведение анализа вариантов структуры больших систем, различных алгоритмов управления изучения влияния изменений параметров системы на ее характеристики и т.д.
1.2. Принципы и методы построения имитационных моделей
Процесс функционирования сложной системы можно рассматривать как смену ее состояний, описываемых ее фазовыми переменными
Z1(t), Z2(t), … Zn(t) в n – мерном пространстве.
Задачей имитационного моделирования является получение траектории движения рассматриваемой системы в n – мерном пространстве (Z1, Z2, … Zn), а также вычисление некоторых показателей, зависящих от выходных сигналов системы и характеризующих ее свойства.
В данном случае “движение” системы понимается в общем смысле – как любое изменение, происходящее в ней.
Известны два принципа построения модели процесса функционирования систем:
1.2.1. Принцип 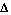 Δt. Рассмотрим этот принцип сначала для детерминированных систем. Предположим, что начальное состояние системы соответствует значениям Z1(t0), Z2(t0), … Zn(t0). Принцип
Δt. Рассмотрим этот принцип сначала для детерминированных систем. Предположим, что начальное состояние системы соответствует значениям Z1(t0), Z2(t0), … Zn(t0). Принцип 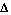 t предполагает преобразование модели системы к такому виду, чтобы значения Z1, Z2, … Zn в момент времени t1= t0
t предполагает преобразование модели системы к такому виду, чтобы значения Z1, Z2, … Zn в момент времени t1= t0 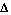 t можно было вычислить через начальные значения, а в момент t2= t1+
t можно было вычислить через начальные значения, а в момент t2= t1+ 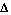 t χчерез значения на предшествующем шаге и так для каждого i-ого шага (
t χчерез значения на предшествующем шаге и так для каждого i-ого шага ( 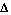 t=const, i=1
t=const, i=1 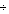 M).
M).
Для систем, где случайность является определяющим фактором, принцип 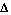 t заключается в следующем:
t заключается в следующем:
1. Определяется условное распределение вероятности на первом шаге (t1= t0+ 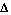 t) для случайного вектора,обозначим его (Z1, Z2, … Zn). Условие состоит в том, что начальное состояние системы соответствует точке траектории
t) для случайного вектора,обозначим его (Z1, Z2, … Zn). Условие состоит в том, что начальное состояние системы соответствует точке траектории  .
.
2. Вычисляются значения координат точки траектории движения системы (t1= t0+ 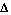 t), к ак значения координат случайного вектора, заданного распределением, найденным на предыдущем шаге.
t), к ак значения координат случайного вектора, заданного распределением, найденным на предыдущем шаге.
3. Отыскиваются условное распределение вектора 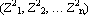 на втором шаге (t2= t1+
на втором шаге (t2= t1+ 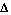 t), при условии получения соответствующих значений
t), при условии получения соответствующих значений 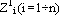 на первом шаге и т.д., пока ti= t0+ i
на первом шаге и т.д., пока ti= t0+ i 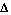 t не примет значения (tМ= t0+ М
t не примет значения (tМ= t0+ М 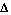 t).
t).
Принцип 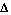 t является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени.
t является универсальным, применим для широкого класса систем. Его недостатком является неэкономичность с точки зрения затрат машинного времени.
1.2.2. Принцип особых состояний (принцип 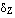 ). При рассмотрении некоторых видов систем можно выделить два вида состояний:
). При рассмотрении некоторых видов систем можно выделить два вида состояний:
· обычное, в котором система находится большую часть времени, при этом Zi(t), (i=1 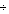 n) изменяются плавно.
n) изменяются плавно.
· особое, характерное для системы в некоторые моменты времени, причем состояние системы изменяется в эти моменты скачком.
Принцип особых состояний отличается от принципа 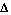 t тем, что шагпо времени в этом случае не постоянен, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.
t тем, что шагпо времени в этом случае не постоянен, является величиной случайной и вычисляется в соответствии с информацией о предыдущем особом состоянии.
Примерами систем, имеющих особые состояния, являются системы массового обслуживания. Особые состояния появляются в моменты поступления заявок, в моменты освобождения каналов и т.д.
Для таких систем применение принципа 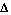 t является нерациональным, так как при этом возможны пропуски особых состояний и необходимы методы их обнаружения.
t является нерациональным, так как при этом возможны пропуски особых состояний и необходимы методы их обнаружения.
В практике использования имитационного моделирования описанные выше принципы при необходимости комбинируют.
1.2.3 пример применения принципа 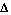 t.
t.
 На рис. 3.2. приведена аналоговая схема дифференцирующего фильтра.
На рис. 3.2. приведена аналоговая схема дифференцирующего фильтра.
Рис. 3.2.
Процесс, происходящий в фильтре, описывается дифференциальным уравнением:

В уравнении:
K- коэффициент усиления,
х(t) – входной сигнал.
Доказано, что 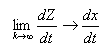
Преобразуем математическую модель фильтра (1) к виду, позволяющему применить принцип 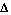 t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:
t. В простейшем случае достаточно уравнение (1) аппроксимировать конечно-разностным уравнением:

Задав начальное условие Z(t0)=Z0 можно построить траекторию процесса, происходящего в фильтре, с целью получения текущего значения производной любой детерминированной функции x(t), подаваемой на вход. Если Вы хотите подробнее узнать как это происходит, нажмите на клавишу ДА.
1.2.4. Пример применения принципа особых состояний.
Рассмотрим магазин мелких подарков “Виртуальный”. В магазине работает один продавец. Требуется имитировать работу магазина с целью изучения перспектив его развития. Из предварительного обследования получена информация, что интервал времени между двумя последовательными приходами покупателей в магазине имеет равномерный закон распределения в интервале ( 1,10 ). Время обслуживания покупателей в магазине также распределено равномерно в интервале (1 ,6 ).
1.2.5. Основные методы имитационного моделирования.
Основными методами имитационного моделирования являются: аналитический метод, метод статического моделирования и комбинированный метод (аналитико-статистический) метод.
Аналитический метод применяется для имитации процессов в основном для малых и простых систем, где отсутствует фактор случайности. Например, когда процесс их функционирования описан дифференциальными или интегродифференциальными уравнениями. Метод назван условно, так как он объединяет возможности имитации процесса, модель которого получена в виде аналитически замкнутого решения, или решения полученного методами вычислительной математики.
Метод статистического моделирования первоначально развивался как метод статистических испытаний (Монте-Карло). Это – численный метод, состоящий в получении оценок вероятностных характеристик, совпадающих с решением аналитических задач (например, с решением уравнений и вычислением определенного интеграла). В последствии этот метод стал применяться для имитации процессов, происходящих в системах, внутри которых есть источник случайности или которые подвержены случайным воздействиям. Он получил название метода статистического моделирования. В параграфах 2-5 данного раздела излагается суть этого метода.
Комбинированный метод (аналитико-статистический) позволяет объединить достоинства аналитического и статистического методов моделирования. Он применяется в случае разработки модели, состоящей из различных модулей, представляющих набор как статистических так и аналитических моделей, которые взаимодействуют как единое целое. Причем в набор модулей могут входить не только модули соответствующие динамическим моделям, но и модули соответствующие статическим математическим моделям.
. Классификация систем по их основным свойствам
Классификация данная в этом параграфе имеет принципиально важное значение, так как используется для построения математических моделей систем. По своим свойствам системы могут быть классифицированы по следующим признакам [7].
Динамические системы характеризуются тем, что их выходные сигналы в данный момент времени определяются характером входных воздействий в прошлом и настоящем (зависит от предыстории). В противном случае системы называют статическими.
Примером динамических систем является биологические, экономические, социальные системы; такие искусственные системы как завод, предприятия, поточная линия и т.д.
Детерминированной называют систему, если ее поведение можно абсолютно точно предвидеть. Система, состояния которой зависит не только от контролируемых, но и от неконтролируемых воздействий или если в ней самой находится источник случайности, носит название стохастической. Приведем пример стохастических систем, это – заводы, аэропорты, сети и системы ЭВМ, магазины, предприятия бытового обслуживания и т.д.
Различают системы линейные и нелинейные. Для линейных систем реакция на сумму двух иди более различных воздействий эквивалентна сумме реакций на каждое возмущение в отдельности, для нелинейных – это не выполняется.
Если параметры систем изменяются во времени, то она называется нестационарной, противоположным понятием является понятие стационарной системы.
Пример нестационарных систем – это системы, где процессы, например, старения являются на данном интервале времени существенными.
Если вход и выход системы измеряется или изменяется во времени дискретно, через шаг ê t, то система называется дискретной. Противоположным понятием является понятие непрерывной системы. Например: ЭВМ, электронные часы, электросчетчик – дискретные системы; песочные часы, солнечные часы, нагревательные приборы и т.д. – непрерывные системы.

рис.1.2. Классификация систем по их свойствам.
(Стрелки указывают возможный набор свойств системы).
1.4. Искусственная система как средство достижения цели
Процесс проектирования любой искусственной системы начинается с формирования цели. Отказ от четкого ее определения заставляет проектировщиков ориентироваться лишь на собственные цели, которые, как правило, связаны со стремлением минимизировать материальные затраты и, возможно, максимизировать доход. И в конечном счете усилия большого коллектива могут быть напрасными, приведут к большим затратам материальных ресурсов, не дадут ожидаемых результатов. Хорошо организованный ночной рейд эскадрильи с воздушным десантом не принесет желаемого успеха боевой операции, если координаты цели неверны.
О значении правильного выбора цели говорит также известный исторический
пример организации противовоздушной обороны английских торговых судов во время второй мировой войны. В качестве цели было выбрано уничтожение вражеских самолетов с помощью зенитных орудий. Так как качающееся палубы судов и недостаточно квалифицированные расчеты артиллеристов на торговых судах не обеспечивали достижения цели, то было решено передать зенитки торговых судов наземным батареям. Однако специалисты во время поняли, что цель должна быть другой, не уничтожение вражеских самолетов, а защита торговых судов. Зенитные установки были оставлены на палубах, в результате немецкие летчики вынуждены были бомбить суда с больших высот и с меньшей точностью. Сокращение потерь судов намного перекрывало затраты на установку и обслуживание орудий.
Одной цели может соответствовать несколько систем и наоборот, одной системе может соответствовать несколько целей. Покажем это на нескольких элементарных примерах, приведенных в таблице 1.2.:
Таблица 1.2.
| Цель функционирования | Система | |
| В любой момент разрезать бумагу, ткань, и т.д. | Ножницы | |
| В любой момент иметь возможность записи текста | Карандаш, авторучка, шариковая ручка | |
| Возможность передачи звуковой информации на расстояния почти мгновенно | Системы радиовещания, телефон | |
| Передача информации на расстояния с большой скоростью | Телеграф, телетайп, сеть “Интернет” | |
| Передача информации на большие расстояния | Системы почтовой связи |
Подводя итоги сказанному можно сформулировать тезис: “система есть средство достижения цели” - Он полностью соответствует назначению и смыслу создания искусственных систем, но для систем природного происхождения он требует ответа на вопрос: Кто, и с какой целью создал Вселенную и человека?
Здесь возможны несколько подходов к ответу на вопрос.
1 Объекты естественного происхождения не являются системами так как, не существовало цели с которой они возникли. В [9] именно так и предлагается поступить с системами естественного происхождения: нет цели – нет системы, это – объекты; например, лес – это объект.
2Определение системы признать правомерным для всех объектов реального мира, но
обсуждаемый тезис считать правомерным только для искусственных систем.
3 Признать существование Того, кто с определенной целью создал весь вселенский мир.
Мы придерживаемся второго варианта. Вся система вселенского пространства вобрала в себя всю “мудрость” развития, накопленную миллиардами лет. Глобальная система систем иерархически выстроенная, с четко отложенной саморегуляцией и саморазвитием формировалась постепенно, изменялась сама и изменяла свои цели в соответствии с Законами Природы. Какова цель существования всех этих взаимодействующих и взаимоподчиненных систем? Это является основным вопросом науки! Возможно глобальная цель связана с самосовершенствованием? Ведь в противном случае вся эта глобальная система систем погибла бы!
Человек и человечество всего лишь составляющая этой единой системы. Тогда становится ясной цель существования человека – самосовершенствование. Таким образом, для гармоничной жизни человеку нужно жить не по своим, придуманным законам, а по объективным Законам Природы, не нарушая их. Только при этом условии можно решить проблемы экологии и устойчивого развития человечества.
Системность как всеобщее свойство материи
Вселенское пространство может быть расема, состоящая из подсистем трех видов – экологических, социальных и искусственных (рис 1.2., 1.3).
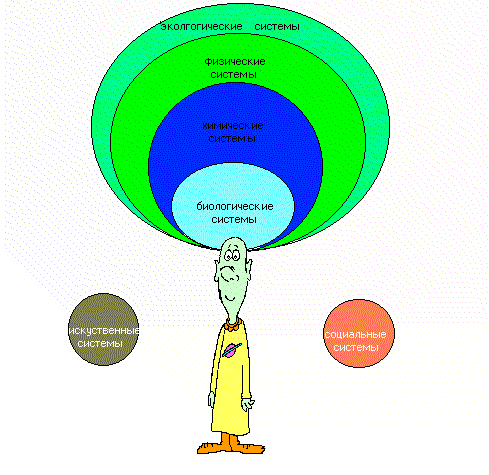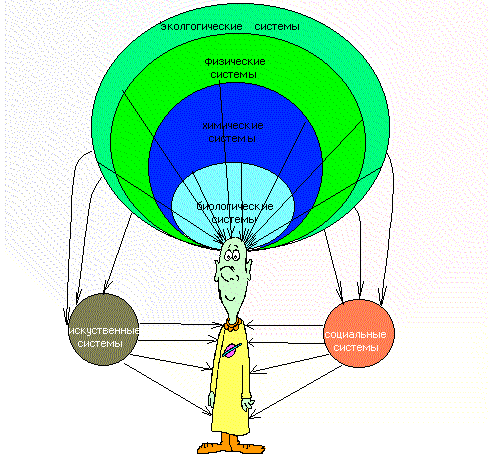 рис. 1.4.
Действие систем вселенского пространства на человека
рис. 1.4.
Действие систем вселенского пространства на человека
|
Экологическая система – это весь материальный мир обитания человека, обеспечивает жизнедеятельность живой материи на Земле и состоит из физических, химических и биологических систем.
Физические системы обеспечивают различные взаимодействия тел и полей, что является непрерывным процессом строительства всего мироздания. Механизмами взаимодействия, функционирования и управления этих систем являются объективные физические законы.
Химические системы осуществляют непрерывный обмен веществ в природе, их преобразование и транспортировку из внешней среды в биологические системы и обратно. Источниками развития этих систем являются вещества; механизмами функционирования – законы физики и химии.
Биологические системы координируют жизнедеятельность всех организмов и их отдельных органов, рост организма, строение, размножение, приспособление к внешней среде и т.д. Источником развития биологических систем являются физические, химические и в том числе и сами биологические системы вселенского пространства.
Социальные системы – это идеально-реальный мир, в котором живет человек (общество, государство, этнос, коллектив, семья, нация, институты, религия, искусства и т.д.). В этих системах люди, взаимодействую друг с другом, создают механизмы и законы жизнеобеспечения. Роль социальных систем заключена в формировании мировоззрения, сознания, культуры, системы человеческих взаимоотношений. Социальные системы формируют модели поведения человека. Человек воспринимает ту модель, которая более всего соответствует его внутреннему содержанию. При этом человек, исходя из своих ценностных ориентаций и возможностей определяет, что он возьмет из предлагаемых моделей поведения. Био-социальный мир существует независимо от конкретного человека и развивается по объективным законам. Причем, если те законы, которые выработаны человечеством в текущий момент времени не соответствуют законам эволюции, то они тормозят эволюционный процесс, в противном случае – наоборот ускоряют его.
Искусственные системы – это системы, созданные человеком в результате научно-технического прогресса. Они предназначены для повышения эффективности труда, его механизации, автоматизации и кибернетизации. Источниками “жизнедеятельности” этих
систем являются все виды систем, перечисленные выше.
Человек занимает особое место среди систем, он не только живет в мире систем, но и сам является системой, персонифицированной составляющей природы (но не ее “царем”). Не смотря на уникальное свойство человека – разум, он живет по законам природы, имеет такие же способы, законы функционирования как вся природа, представляя из себя сложную физико-химико-биологическую систему саморегуляции. Его “системность” многогранна и, наприме, проявляется в его деятельности в процессе создания технических, организационных и социальных систем и пронизывает все сферы его жизни. Системность деятельности человека определяется алгоритмичностью. Ее суть -разработка плана действий в виде системы взаимосвязанных мероприятий для достижения определенных целей. Эта деятельность может носить как простой характер так и сложный: принятие управленческих решений, решение научных задач, задач проектирования и т.д. Но в любом случае она носит ярко выраженный системный характер. В ней всегда существует оценка ситуации, определение степени актуальности проблемы, целей, представление решения проблемы в виде определенных действий, оценка альтернатив, осуществление процесса решения, оценка результата с точки зрения его последствий.
Все названные виды систем функционально связаны между собой в единое, которое и образует вселенское пространство как всеобщую систему. Вместе с тем каждая система автономна, выполняет свою уникальную функцию, имеет свои источники, механизмы и законы развития. Современный уровень развития науки позволяет говорить о мире как о бесконечной иерархической системе систем, находящихся на разном уровне иерархии и разных стадиях развития.
Простые системы входят составной частью в более сложные. Функции сложной системы – обеспечить условия “жизнеобеспечения” своих подсистем. Функции подсистемы – выработать энергию и обеспечить ею систему, в которую она входит.
Природные, социальные процессы свидетельствуют о том, что системы, отдавая свою энергию и заимствуя ее у других, стремится к максимальному самосохранению.
То есть системы с одной стороны не могут существовать без других систем, путем установления между ними связи для информационного, энергетического и материального обмена, а с другой – стремятся к самостоятельности, минимизации потерь от этих связей.
Таким образом, весь мир системен и системность является свойством материи
Может быть Б3 В1Имитационное моделирование систем и процессов.
Применяется в случаях, когда нельзя заформализовать модель (описать аналитическим выражением) и в случае, когда система представляет собой многопараметрическую вероятностную экономическую систему. Кроме того, моделирование с помощью имитационных подходов применяется для систем больших размерностей и с большими внутренними связями.
Основные этапы моделирования:
1) анализ моделируемой систем, сбор необходимой информации, выделение проблемной области исследования и постановка задач на исследование;
2) синтезирование (формирование, получение) необходимой математической модели области допустимых упрощений (ограничений), выбор критериев оценки эффективности и точности моделирования; 3 разработка имитационной модели, алгоритма ее реализации, внутреннее и внешнее математическое обеспечение;4 оценка адекватности имитационной модели и контроль результатов экстремумов с последующей валидацией модели; 5 анализ результатов моделирования с целью достижения заданной точности моделирования.
Имитационная модель и ее структура..

При создании модели необходимо максимально использовать те параметры системы, которые поддаются формализации, то есть записи с помощью
Дата добавления: 2015-01-19; просмотров: 524; Мы поможем в написании вашей работы!; Нарушение авторских прав |