
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Существующие подходы к визуальному моделированию сложных динамических систем
В настоящее время существует великое множество визуальных средств моделирования. Договоримся не рассматривать в этой работе пакеты, ориентированные на узкие прикладные области (электроника, электромеханика и т.д.), поскольку, как отмечалось выше, элементы сложных систем относятся, как правило, к различным прикладным областям. Среди оставшихся универсальных пакетов (ориентированных на определенную математическую модель), мы не будем обращать внимание на пакеты, ориентированные на математические модели, отличные от простой динамической системы (уравнения в частных производных, статистические модели), а также на чисто дискретные и чисто непрерывные. Таким образом, предметом рассмотрения будут универсальные пакеты, позволяющие моделировать структурно-сложные гибридные системы.
Их можно условно разделить на три группы:
1) пакеты "блочного моделирования":
2) пакеты "физического моделирования":
3) пакеты, ориентированные на схему гибридного автомата.
Это деление является условным прежде всего потому, что все эти пакеты имеют много общего: позволяют строить многоуровневые иерархические функциональные схемы, поддерживают в той или иной степени технологию ООМ, предоставляют сходные возможности визуализации и анимации. Отличия обусловлены тем, какой из аспектов сложной динамической системы сочтен наиболее важным.
Пакеты "блочного моделирования" ориентированы на графический язык иерархических блок схем. Элементарные блоки являются либо предопределенными, либо могут конструироваться с помощью некоторого специального вспомогательного языка более низкого уровня. Новый блок можно собрать из имеющихся блоков с использованием ориентированных связей и параметрической настройки. В число предопределенных элементарных блоков входят чисто непрерывные, чисто дискретные и гибридные блоки.
К достоинствами этого подхода следует отнести, прежде всего, чрезвычайную простоту создания не очень сложных моделей даже не слишком подготовленным пользователем. Другим достоинством является эффективность реализации элементарных блоков и простота построения эквивалентной системы. В то же время при создании сложных моделей приходится строить довольно громоздкие многоуровневые блок-схемы, не отражающие естественной структуры моделируемой системы. Другими словами, этот подход работает хорошо, когда есть подходящие стандартные блоки.
Наиболее известными представителями пакетами "блочного моделирования" являются:
- подсистема SIMULINK пакета MATLAB (MathWorks, Inc.; http://www.mathworks.com/);
- EASY5 (Boeing)
- подсистема SystemBuild пакета MATRIXX (Integrated Systems, Inc. );
- VisSim (Visual Solution; http://www.vissim.com/).
Пакеты "физического моделирования" позволяют использовать неориентированные и потоковые связи. Пользователь может сам определять новые классы блоков. Непрерывная составляющая поведения элементарного блока задается системой алгебро-дифференциальных уравнений и формул. Дискретная составляющая задается описанием дискретных событий (события задаются логическим условием или являются периодическими), при возникновении которых могут выполняться мгновенные присваивания переменным новых значений. Дискретные события могут распространяться по специальным связям. Изменение структуры уравнений возможно только косвенно через коэффициенты в правых частях (это обусловлено необходимостью символьных преобразований при переходе к эквивалентной системе).
Подход очень удобен и естественен для описания типовых блоков физических систем. Недостатками являются необходимость символьных преобразований, что резко сужает возможности описания гибридного поведения, а также необходимость численного решения большого числа алгебраических уравнений, что значительно усложняет задачу автоматического получения достоверного решения.
К пакетам "физического моделирования" следует отнести:
"20-SIM" (Controllab Products B.V; http://www.rt.el.utwente.nl/20sim/);
- Dymola (Dymasim; http://www.dynasim.se/);
- Omola, OmSim (Lund University; http://www.control.lth.se/~cace/omsim.html);
Как обобщение опыта развития систем этого направления междунородной группой ученых разработан язык Modelica (The Modelica Design Group; http://www.dynasim.se/modelica), предлагаемый в качестве стандарта при обмене описаниями моделей между различными пакетами.
Пакеты, основанные на использовании схемы гибридного автомата, позволяют очень наглядно и естественно описывать гибридные системы со сложной логикой переключений. Необходимость определения эквивалентной системы при каждом переключении заставляет использовать только ориентированные связи. Пользователь может сам определять новые классы блоков. Непрерывная составляющая поведения элементарного блока задается системой алгебро-дифференциальных уравнений и формул. К недостаткам следует также отнести избыточность описания при моделировании чисто непрерывных систем.
К этому направлению относится пакет Shift (California PATH: http://www.path.berkeley.edu/shift), а также отечественный пакет Model Vision Studium. Пакет Shift в большей стпени ориентирован на описание сложных динамических структур, а пакет MVS - на описание сложных поведений.
Заметим, что между вторым и третьим направлениями нет непреодолимой пропасти. В конце концов, невозможность из совместного использования обусловлена лишь сегодняшними вычислительными возможностями. В то же время, общая идеология построения моделей практически совпадает. В принципе, возможен комбинированный подход, когда в структуре модели должны выделяться составные блоки, элементы которых имеют чисто непрерывное поведение, и однократно преобразовываться к эквивалентному элементарному. Далее уже совокупное поведение этого эквивалентного блока должно использоваться при анализе гибридной системы.
Б5В1Метод Монте-Карло (метод статистических испытаний).
Данный метод родился в 1949 году благодаря усилиям американских ученых Дж. Неймана и Стива Улана в городе Монте-Карло (княжество Монако).
Метод Монте-Карло – численный метод решения математических задач при помощи моделирования случайных чисел.
Суть метода состоит в том, что посредствам специальной программы на ЭВМ вырабатывается последовательность псевдослучайных чисел с равномерным законом распределения от 0 до1. Затем данные числа с помощью специальных программ преобразуются в числа, распределенные по закону Эрланга, Пуассона, Релея и т.д.
Полученные таким образом случайные числа используются в качестве входных параметров экономических систем :
Q (x1, x2, x3,…,xn) Þ Qpt (min или max)
 W: Bs (x1, x2, x3,…,xn) £ Rs
W: Bs (x1, x2, x3,…,xn) £ Rs
При многократном моделировании случайных чисел, которые мы используем в качестве входных параметров системы (модели), определяем математическое ожидание функции M(Q) и, при достижении средним значением функции Q уравнения не ниже заданного, прекращаем моделирование.
Статистические испытания (метод Монте-Карло) характеризуются основными параметрами:
D - заданная точность моделирования;
P – вероятность достижения заданной точности;
N – количество необходимых испытаний для получения заданной точности с заданной вероятностью.
Определим необходимое число реализаций N, тогда
(1 - D) будет вероятность того, что при одном испытании результат не достигает заданной точности D;
(1 - D) N – вероятность того, что при N испытаниях мы не получим заданной точности D.
Тогда вероятность получения заданной точности при N испытаниях можно найти по формуле
 (19)
(19)
Формула (19) позволяет определить заданное число испытаний для достижения заданной точности D с заданной вероятностью Р.
| D | Значение Р | |||
| 0,80 | 0,20 | 0,95 | 0,99 | |
| 0,10 0,05 0,025 0,0125 0,006 |
êQi – Qконеч êÞ D
Случайные числа получаются в ЭВМ с помощью специальных математических программ или спомощью физических датчиков. Одним из принципов получения случайных чисел является алгоритм Неймана, когда из одного случайного числа последовательно выбирается середина квадрата
g0 = 0,9876 g0 2 = 0,97531376
g1 = 0,5313 g12 = 0,28654609
g2 = 0,6546 g22 = 0,42850116 и т.д.
Кроме того данные числа проверяются на случайность и полученные числа заносятся в базу данных.
Физические датчики разрабатываются на электронных схемах и представляют собой генераторы белого (нормального) шума, то есть когда в спектральном составе шума имеются гармоничные составляющие с частотой F ®¥. Из данного белого шума методом преобразования получаются случайные числа.
Основные понятия системного подхода и анализа.
При анализе сложных экономических систем (СЭС) придерживаются системного подхода. Это предполагает максимальный охват всех взаимосвязей и анализ последствий принятого решения.
Основные моменты:
а) Уточнение предметной области исследования, ее структуризация на задачи; б) выбор параметров и критериев оценки эффективности системы; в) Подбор нужных ЭММ; г) Уточнение деталей и целей анализа системы; д) Синтезирование математических моделей, обеспечивающих достижение поставленных целей.
Системы в своем структурном строении бывают одноуровневые и многоуровневые.

Б12 В1Классификация систем и их моделей.
Формальная классификация моделей.
| Признак классификации | Модель |
| 1. Целевое назначение | Прикладные, теоретико-аналитические |
| 2. По типу связей | Детерминированные, стохастические |
| 3. По фактору времени | Статические, динамические |
| 4. По форме показателей | Линейные, нелинейные |
| 5. По соотношению экзогенных и эндогенных переменных | Открытые, закрытые |
| 6. По типу переменных | Дискретные, непрерывные, смешанные |
| 7. По степени детализации | Агрегированные (макромодели), детализированные (микромодели) |
| 8. По количеству связей | Одноэтапные, многоэтапные |
| 9. По форме представления информации | Матричные, сетевые |
| 10. По форме процесса | Аналитические, графические, логические |
| 11. По типу математического аппарата | Балансовые, статистические, оптимизационные, имитационные, смешанные |
В зависимости от признаков системы, сами системы и их модели классифицируются на:
1)  динамические и статические; 2 стохастические (вероятностные) и детерминированные (регулярные); 3 непрерывные и дискретные; 4 линейные и нелинейные. По наличию обратных связей системы подразделяются на открытые, закрытые, комбинированные.
динамические и статические; 2 стохастические (вероятностные) и детерминированные (регулярные); 3 непрерывные и дискретные; 4 линейные и нелинейные. По наличию обратных связей системы подразделяются на открытые, закрытые, комбинированные.
Открытые:
Закрытые:
Комбинированные:
Особенности экономических систем.
Экономическая система является частью более сложной системы – социально-экономической, и представляет собой вероятностную, динамическую, адаптивную систему, охватывающую процессы производства, обмена, распределения и потребления материальных благ, а также предоставления различных сервисных услуг. Как правило, входные параметры экономических систем – это материальные вещественные потоки производственных и природных ресурсов, то есть Х. Входные параметры – это материальные вещественные потоки, оборудование, военная продукция, продукция накопления, возмещения и экспорта, то есть У.
Экономические системы – многоступенчатые, многоуровневые системы, и любая неопределенность, случайность во входных параметрах в нижних уровнях приводит к неопределенностям и случайностям в выходных параметрах подсистем более высокого порядка и системы в целом.
Структурная схема простой экономической системы

 ЭММ оптимизации обычной экономической системы
ЭММ оптимизации обычной экономической системы
где pi – прибыль от реализации единицы продукции;
xi - объем выпуска продукции;
ai - расход сырья на единицу продукции;
B - общий запас сырья;
W - область допустимых ограничений;
Понятие о вероятностных системах и процессах.
Экономические системы, как правило, являются вероятностными (стохастическими), так как выходные параметры системы случайным образом зависят от входных параметров.
Почему экономические системы являются стохастическими: так как система сложная, многокритериальная многоуровневая иерархическая структура; система подвержена влиянию внешних факторов (погодные условия, внешняя политика); преднамеренное искажение информации, сокрытие информации и целенаправленная экономическая диверсия. Исходя из того, что экономическая система сложная и имеет случайную компоненту e,
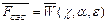
поэтому оптимизация целевой функции ведется по среднему значению, то есть при заданных параметрах a необходимо найти решение хÎC, когда значение целевой функции по возможности будет максимальным.
Сложные системы описываются Марковским аппаратом, то есть когда поведение системы в момент t0 характеризуется вероятностью первого порядка p(х0, t0) и поведение системы в будущем зависит от значения системы х0 и не зависит от того, когда и как система пришла в это состояние.
Марковские случайные процессы описываются двумя параметрами:
1) вероятностью первого порядка p(х0, t0); условной вероятностью pij (х2 t2 /х1 t1);
pij характеризует значение системы х2 в момент t2, при условии, что в момент t1 система имела значение х1.
Имея в своем распоряжении матрицу условных переходов
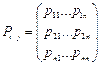
можно заранее сформулировать поведение системы в будущем.
Марковские случайные процессы называют Марковскими цепями с вероятностью перехода в pij, когда процесс изучается в дискретные моменты времени.
Б17 В3Основные понятия об эконометрических моделях и корреляционном анализе.
Эконометрические модели являются составляющими более широкого класса ЭММ. Данная модель выступает в качестве средств анализа и прогнозирования конкретных экономических процессов, как на макро, так и на микро уровнях на основе реальной статистики.
Эконометрическая модель, учитывая корреляционные связи, позволяет путем подбора аналитической зависимости построить модель на базисном периоде и при достаточной адекватности модели использовать ее для краткосрочного прогноза.
При синтезе эконометрических моделей при имеющихся факторных признаках xi и результативных параметрах yi необходимо определить a0, a1, a2, a3, …,an.
yi = f(xi) + ei, где
f(xi) – величина детерминированная;
ei, yi – величины случайные.
Эконометрическая модель опирается на понятие корреляционных связей и так называемое уравнение регрессии.
Корреляционная связь – когда при одном и том же значении факторного признака х встречаются разные значения у. Корреляционные связи описываются так называемыми уравнениями регрессии.
Уравнение регрессии – уравнение прямой (как и любой кривой), описывающее корреляционную связь, а сама прямая (кривая) называется линией регрессии.
Корреляционные связи оцениваются по среднему значению всей совокупности результативного признака, такт как для одного и того же значения факторного признака возможны различные значения результативного признака.
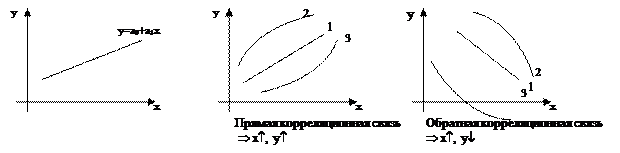 |
Корреляционные связи (уравнения регрессии), а также эконометрические модели, построенные на базе уравнения регрессии, могут описываться:
1) уравнением прямой: yi = a0 + a1x
2) уравнением 2-го порядка: yi = a0 + a1x + a2x2
3) уравнением показательной функции: yi = a0a1x
4) уравнением степенной функции: yi = a0xa1
5) уравнением гиперболы: yi = a0 + a11/x
При построении эконометрических моделей нам известны фактические значения х и у, а нам необходимо определить параметры a0 , a1, a2 для соответствующей модели. Данные параметры определяются по методу наименьших квадратов.
Б19В1 Понятие сложной системы. Сложная система – комплекс подсистем, обладающих общими сложными свойствами.
Элемент системы при данном подходе – это тот объект, который не подлежит расчленения, и внутренняя структура которого не исследуется. Сложные системы, их структура и иерархия определяются целями исследования.
Подсистема – самостоятельно функционирующий объект, не подлежащий декомпозиции.
Принципы выделения системы: наличие управляющего центра; обладает общей целью; состоит из компонентов; система работает при взаимодействии с окружающей средой; система жизнеспособна при наличии достаточных ресурсов.
Взаимодействие системы с внешней средой
Любая техническая, биологическая система работает в окружении среды, которая оказывает внешнее воздействие на систему с параметрами возмущения, искажающими результаты управления.

Параметры:
X – входные параметры, факторные признаки, экзогенные параметры;
Y – выходные параметры, результативные признаки, эндогенные параметры;
Z – параметры возмущения, случайные факторы, случайные составляющие;
U – параметры управления. Системы бывают открытые (взаимодействующие с внешней средой) и закрытые (невзаимодействующие с внешней средой).
Особенности сложных систем.
Сложная система – комплекс отдельных подсистем, функционирующих в тесном взаимодействии, решающих общую задачу.
Основные особенности: наличие большого количества связанных между собой отдельных подсистем; наличие иерархической структуры управления, как по горизонтали, так и по вертикали; обязательной присутствие информационной сети; функционирование связано с воздействием случайных факторов.
Эффективность системы определяется функционалом:
W = F0 (f(x0), f(x1),…,f(xn))
Б23В1 Основные понятия и определения.
Система массового обслуживания (СМО) – это совокупность приборов, каналов, станков, линий обслуживания, на которые в случайные или детерминированные моменты времени поступают заявки на обслуживание. Например, коммутаторы телефонных станций, супермаркет, парикмахерские.
Оптимизация и оценка эффективности СМО состоит в нахождении средних суммарных затрат на обслуживание каждой заявки и нахождение средних суммарных потерь от заявок не обслуженных.
СМО состоит из определенного числа обслуживающих каналов и предназначена для выполнения заявок с разным характером распределения момента времени на обслуживание.
Моделирование СМО предполагает:
1) построение ЭММ, связывающих параметры СМО (число каналов, их производительность и т.п.) с показателями эффективности;
2) оптимизацию данных показателей с целью получения максимальной эффективности.
Классификация и обозначение СМО.
По ряду признаков СМО делятся на:
1. СМО: - с очередями; с отказами заявок (очереди);
2. СМО с очередью: - в порядке очереди; - в случайном порядке; обслуживание с приоритетом (абсолютным или относительным);
3. СМО с многофазным обслуживанием;
4. СМО:- закрытые (замкнутые) – поток заявок генерируется самой системой;
- открытые – характер потока заявок не зависит от состояния СМО;
5. СМО:- одноканальные; многоканальные.
Обозначения СМО.
Для сокращения записи и характеристик СМО принята общемировая система записи по формату Кендола.
( a ç b ç c ç) : ( d çe çf )
a –характеризует закон распределения заявок входного потока;
b - характеризует закон распределения интервалов выполнения заявок на обслуживание;
c - характеризует количество каналов обслуживания;
d - характеризует дисциплину очереди;
e - характеризует максимальное количество требований (заявок) на обслуживание (е в очереди + е в обслуживании);
f – максимальный объем источника (генератора) заявок.
Пример.
GI çG ç N
GI - данная позиция характеризует, что момент заявок, поступающих на обслуживание, распределен по случайному закону с функцией распределения F(x) с математическим ожиданием  .
.
F(x) – любой закон распределения;
G - данная позиция характеризует моменты распределения (временные интервалы) обслуживания заявок с любой функцией распределения H(x) и со средним временем обслуживания  .
.
( M1 ç M2 ç N ) : - характеризует, что поток заявок, поступающих на обслуживание как входящий поток, подчиняется закону Пуассона с функцией распределения 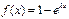 ,
,
l - интенсивность потока заявок;
M1 – простейший поток заявок;
N – количество мест по обслуживанию заявок;
M2 – характеризует поток обслуживания и распределения времени обслуживания также по простейшему Пуассоновскому закону с функцией распределения  ,
,
m - характеризует интенсивность потока обслуживания.
Простейший поток обладает тремя свойствами:
1) стационарностью;
2) безпоследействия;
3) ординарностью.
Стационарность – это когда вероятность попадания того или иного числа заявок на интервал времени длиной t зависит от длины этого интервала и не зависит от того, где этот интервал расположен на оси времени.
Поток безпоследействия – когда для любых не перекрывающихся участков времени число заявок, попадающих на один из участков, не зависит от числа заявок, попадающих на другой участок.
Ординарность – это когда вероятность попадания на участок t двух или более заявок пренебрежимо мала по сравнению с вероятностью попадания одной заявки.
Поток, обладающий вышеназванными тремя свойствами, называется простейшим (стационарным, Пуассоновским ) потоком.
Эрланговский поток – “просеянный” простейший поток с коэффициентом k = (2;3;4...), то есть когда обслуживается каждая 2,3,...,k заявка.
El êEm êNM – эрланговский входной поток заявок El и эрланговский закон обслуживания Em.
Основные характеристики системы массового обслуживания.
Характеристиками, принятыми для СМО, являются:
1) вероятность потери заявок Ротказа = Рпотерь
2) вероятность занятости k каналов Рк
3) среднее число занятых каналов 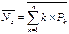 4. коэффициент простоя каналов
4. коэффициент простоя каналов  N0 – незанятых каналов, n – всего каналов.
N0 – незанятых каналов, n – всего каналов.
5средняя длина очереди

6 среднее число требований, находящихся на обслуживании 
Эффективность СМО можно определить, используя следующую методику:
(*) ЕСМО = 
qожид –потери в результате ожидания 1 заявки в единицу времени;
qnk – стоимость простоя одного канала в единицу времени;
qk - стоимость эксплуатации одного канала в единицу времени;
(*) – показывает один из возможных подходов к оценке эффективности СМО. Как правило для высокоточных оценок эффективности используются имитационные модели.
Дата добавления: 2015-01-19; просмотров: 467; Мы поможем в написании вашей работы!; Нарушение авторских прав |