Пояснения к рабочей программе

При изучении темы «Колебания» следует параллельно рассматривать механические и электромагнитные колебания, что способствует выработке у студента единого подхода к колебаниям различной физической природы. Здесь следует четко уяснить понятия фазы, разности фаз, амплитуды, частоты, периода колебаний и там, где это необходимо, использовать графический метод представления гармонического колебания. Нужно уяснить, что любые колебания линейной системы всегда можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными частотами, амплитудами и начальными фазами.

Изучение темы «Волны» целесообразно начинать с механических волн, распространяющихся в упругих средах. Здесь следует обратить внимание на картину мгновенного распределения смещений и скоростей в бегущей волне, различие между бегущей и стоячей волнами, зависимость фазовой скорости от частоты колебаний, найти связь между групповой и фазовой скоростями и показать их равенство в отсутствие дисперсии волн. Особое внимание студент должен уделить условию интерференции волн, энергетическому соотношению при когерентности волн, понять и объяснить перераспределение энергии при образовании минимумов и максимумов интенсивности. Переходя к изучению электромагнитных волн, студенту следует ясно представить себе физический смысл уравнений Максвелла и, опираясь на них, рассмотреть свойства этих волн. Нужно четко представлять, что переменные электрическое и магнитное поля взаимосвязаны, они поддерживают друг друга и могут существовать независимо от источника, их породившего, распространяясь в пространстве в виде электромагнитной волны. Другими словами, электромагнитная волна – это распространяющееся в пространстве переменное электромагнитное поле. Под энергией электромагнитного поля следует подразумевать сумму энергий электрического и магнитного полей. Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь. Следует помнить, что если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

В настоящее время волновая оптика является частью общего учения о распространении волн. При изучении явлений интерференции, дифракции, объясняемых с позиций волновой природы света, студент должен обратить внимание на общность этих явлений для волн любой природы. Но световые волны имеют специфические особенности, когерентность, монохроматичность, которые обусловлены конечной длительностью свечения отдельного атома.

При изучении интерференции света особое внимание следует обратить на такие вопросы, как цвета тонких пленок, полосы равной толщины и равного наклона. Следует помнить, что при интерференции света имеет место суперпозиция, связанная с перераспределением энергии, а не с взаимодействием волн.

Рассматривая явление дифракции, необходимо уяснить метод зон Френеля, уметь пользоваться графическим методом сложения амплитуд, что будет способствовать пониманию дифракции как на одной щели, так и на дифракционной решетке. Кроме того, необходимо изучить дифракцию на пространственной решетке и уметь пользоваться формулой Вульфа–Брэгга, являющейся основной в рентгеноструктурном анализе, имеющем важнейшее практическое применение.

Изучение явлений интерференции и дифракции света должно подготовить студента к пониманию основ волновой (квантовой) механики и физики твердого тела.

Поперечность световых волн была экспериментально установлена при изучении явления поляризации света, которое имеет большое практическое применение. При изучении этого явления особое внимание следует обратить на способы получения поляризованного света и применение законов Брюстера, Малюса, на явление вращения плоскости поляризации в кристаллах и растворах, эффект Керра.

Изучая явление дисперсии света, необходимо уяснить сущность электронной теории этого явления, отличие нормальной дисперсии от аномальной.

Следует представлять, что при движении заряженных частиц в веществе в том случае, когда их скорость движения превышает фазовую скорость световых волн в этой среде, возникает излучение Вавилова–Черенкова, которое нужно рассматривать как классическое явление.

Переход от классической физики и квантовой связан с проблемой теплового излучения и, в частности, с вопросом распределения энергии по частотам в спектре абсолютно черного тела. При изучении квантовой природы излучения, необходимо знать гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана–Больцмана и Вина.

Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света получили название фотонов. С позиций квантовой теории света объясняются такие явления, как фотоэлектрический эффект и эффект Комптона. При изучении фотоэффекта следует знать формулу Эйнштейна и на ее основании уметь объяснить закономерности, установленные Столетовым.

Рассматривая эффект Комптона, необходимо обратить внимание на универсальный характер законов сохранения, которые оказываются справедливыми в каждом отдельном акте взаимодействия фотона с электроном.

Изучая световое давление, важно понять, что это явление может быть объяснено как на основе волновых представлений о свете, так и с точки зрения квантовой теории.

В итоге изучения этого раздела у студента должно сформироваться представление, что электромагнитное излучение имеет двойственную корпускулярно-волновую природу (корпускулярно-волновой дуализм). Корпускулярно-волновой дуализм является проявлением взаимосвязи двух основных форм материи: вещества и поля.

Контрольная работа № 3 построена таким образом, чтобы проверить знания студентов по разделу «Колебания. Волны. Оптика».

Задачи на гармонические колебания охватывают такие вопросы, как определение амплитуды, скорости, ускорения, энергии, периода механических колебаний, силы тока, напряжения, энергии и частоты электромагнитных колебаний.

Волновые процессы представлены задачами, в которых определяются частота, длина, скорость распространения, энергия и объемная плотность энергии механических и электромагнитных волн.

Задачи по теме «Интерференция света» включают расчет интерференционной картины от двух когерентных источников, интерференцию в тонких пленках, полосы равной толщины и равного наклона.

Тема «Дифракция света» представлена задачами на темы: зоны Френеля, дифракция в параллельных лучах на одной щели, на плоской и пространственной дифракционных решетках, разрешающая способность дифракционной решетки.

Задачи по теме «Поляризация света» охватывают такие вопросы, как применение законов Брюстера, Малюса, определение степени поляризации, вращение плоскости поляризации в растворах и кристаллах.

Тема «Распространение света в веществе» включает законы теплового излучения, фотоэффект, эффект Комптона, давление света.

ОСНОВНЫЕ ФОРМУЛЫ

Уравнение гармонического колебания: ,

где А – амплитуда колебания, ω – циклическая частота, φ₀ – начальная фаза.

Период колебаний маятников:

пружинного ;

физического ;

где m – масса маятника, k – жесткость пружины, J – момент инерции маятника, g – ускорение свободного падения, l – расстояние от точки подвеса до центра масс.

Период колебаний в электрическом колебательном контуре:

,

где L – индуктивность контура, С – емкость конденсатора.

Уравнение плоской волны, распространяющейся в направлении оси Ox:

,

где 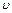– скорость распространения волны.

Длина волны: ,

где Т – период волны.

Скорость распространения электромагнитной волны: ,

где с – скорость света в вакууме, ε – диэлектрическая проницаемость среды, μ – магнитная проницаемость.

Скорость распространения звука в газе, при постоянном давлении и объеме: ,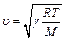

где γ – отношение теплоемкостей газа, при постоянном давлении и объеме, R – молярная газовая постоявшая, Т – термодинамическая температура, М – молярная масса газа.

Вектор Пойнтинга: ,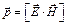

где 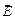и 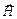– напряженности электрического и магнитного полей электромагнитной волны.

Оптическая длина пути в однородной среде: ,

где s – геометрическая длина пути световой волны, n – показатель преломления среды.

Оптическая разность хода: ,

где l₁ и l₂ – оптические пути двух световых волн.

Условие интерференционного максимума: ,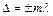

и интерференционного минимума: ,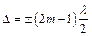

Ширина интерференционных полос в опыте Юнга: ,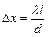

где d – расстояние между когерентными источниками света, l – расстояние от источников до экрана.

Оптическая разность хода в тонких пленках:

в проходящем свете: ;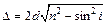

в отраженном свете: ;

где d – толщина пленки, i – угол падения света.

Радиусы светлых колец Ньютона в проходящем свете или темных в отраженном: ,

и темных колец в проходящем свете или светлых в отраженном:

,

где R – радиус кривизны линзы, λ – длина световой волны в среде.

Радиусы зон Френеля

для сферической волновой поверхности: ,

для плоской волновой поверхности: ,

где а – радиус волновой поверхности, b – кратчайшее расстояние от волновой поверхности до точки наблюдения.

Условия направления ифракционных максимумов от одной щели :

,

и дифракционных минимумов: ,

где а – ширина щели.

Определение направлений на главные максимумы дифракционной решетки:

,

где d – постоянная дифракционной решетки.

Разрешающая способность дифракционной решетки: ,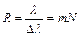

где ∆λ – минимальная разность длин волн двух, спектральных линий, разрешаемых решеткой, m – порядок спектра, N – общее число щелей решетки.

Формула Вульфа–Брэгга: ,

где d – расстояние между атомными плоскостями кристалла, θ_m – угол скольжения рентгеновских лучей.

Степень поляризации: ,

где I_max и I_min – максимальная и минимальная интенсивность света.

Закон Брюстера: ,

где i_Б – угол Брюстера, n₁ и n₂ – показатели преломлений первой и второй среды.

Закон Малюса: ,

где I_о и I – интенсивности плоскополяризованного света, падающего и прошедшего через поляризатор, α – угол между плоскостью поляризации падающего света и главной плоскостью поляризатора.

Угол поворота плоскости поляризации света:

в кристаллах и чистых жидкостях: ,

в растворах: ,

где φ₀ – постоянная вращения, [φ₀] – удельная постоянная вращения, C – концентрация оптически активного вещества в растворе, l – расстояние, пройденное светом в оптически активном веществе.

Фазовая скорость света в веществе: ,

где с – скорость света в вакууме.

Дисперсия вещества: .

Групповая скорость света: .

Направление излучения Вавилова–Черенкова: ,

где 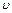– скорость заряженной частицы.

Закон Стефана–Больцмана: ,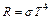

где R – энергетическая светимость черного тела, Т – термодинамическая температура тела, σ – постоянная Стефана–Больцмана.

Закон смещения Вина: ,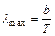

где λ_max – длина волны, на которую приходится максимум энергии излучения черного тела, b – постоянная Вина.

Давление света при нормальном падении на поверхность:

,

где I – интенсивность света, 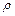– коэффициент отражения, w – объемная плотность энергии излучения.

Энергия фотона: ,

где h – постоянная Планка, 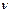– частота световой волны.

Уравнение Эйнштейна для внешнего фотоэффекта:

,

где А – работа выхода электронов из металла, Т_max – максимальная кинетическая энергия фотоэлектронов.

Комптоновская длина волны частицы: ,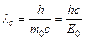

где m₀ – масса покоя частицы, Е₀ – энергия покоя частицы.

Изменение длины волны рентгеновского излучения при эффекте Комптона: ,

где λ и λ^’ – длина волны падающего и рассеянного излучения, θ – угол рассеяния.