Пояснения к рабочей программе. Изучение этого раздела следует начать с элементов квантовой механики и рассмотреть такие вопросы, как корпускулярно-волновой дуализм материи

Изучение этого раздела следует начать с элементов квантовой механики и рассмотреть такие вопросы, как корпускулярно-волновой дуализм материи, гипотезу де Бройля, уяснить, что движение любой частицы согласно этой гипотезе всегда сопровождается волновым процессом. Исходя из соотношений неопределенностей Гейзенберга, определить границы применимости классической механики и понять, что из этих соотношений вытекает необходимость описания состояния микрочастиц с помощью волновой функции, обратить внимание на ее статистический смысл. Целесообразно рассмотреть применение уравнения Шредингера к стационарным состояниям (прямоугольная потенциальная яма бесконечной глубины), следует знать правила квантования энергии, орбитального момента импульса в атоме водорода и выяснить смысл трех квантовых чисел. При изучении темы «Периодическая система элементов» необходимо обратить внимание на физический смысл спинового числа и принцип запрета Паули, на основе которого рассмотреть распределение электронов в атоме по состояниям.

Переходя к изучению элементов физики атомного ядра и элементарных частиц, студент должен хорошо представлять себе состав атомного ядра и его характеристики: массу, линейные размеры, момент импульса, магнитный момент ядра, дефект массы ядра, энергию и удельную энергию связи ядра. Рассматривая состав ядра и взаимодействие нуклонов в ядре, нужно знать свойства ядерных сил и обратить внимание на их обменную природу.

В процессе изучения радиоактивного распада ядер важно понять дискретный характер энергетического спектра α-частиц и γ-излучения, свидетельствующий о квантовании энергии ядер; понять закономерности β-распада, связанного с законами сохранения энергии и момента импульса.

Изучая тему «Ядерные реакции», важно понять, что во всех ядерных реакциях выполняются законы сохранения: энергии, импульса, момента импульса, электрического заряда, числа нуклонов. Особое внимание уделите реакциям синтеза легких и делению тяжелых ядер, вопросам ядерной энергетики и проблемам управления термоядерными реакциями.

При изучении темы «Элементы физики твердого тела» основное внимание должно быть уделено: элементам теории кристаллической решетки, элементам зонной теории твердых тел, полупроводникам, проводникам (металлам). Рассматривая эти вопросы, существенно понять характер теплового движения в твердых телах, дебаевскую теорию теплоемкости, распределение электронов по энергиям при Т=0 и Т>0, иметь качественное представление о сверхпроводимости, выяснить различие между металлами, диэлектриками и полупроводниками, рассмотреть собственную и примесную проводимости полупроводников и вольтамперную характеристику р – n -перехода.

Кроме тем, затронутых в предыдущем разделе, контрольная работа № 3 представлена набором задач, включающих также следующие вопросы: определение длины волны де Бройля движущихся частиц, соотношения неопределенностей Гейзенберга, применение уравнения Шредингера для частицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками, рентгеновское излучение и закон Мозли, закон радиоактивного распада, определение дефекта массы, энергии связи и удельной энергии связи ядра, энергии ядерных реакций. В эту контрольную работу включены также задачи по теме: «Элементы физики твердого тела», в которых определяются параметры объемно-центрированных и гранецентрированных кубических решеток, удельная и молярная теплоемкости при постоянном объеме по теории Дебая при Т<<θ_D, примесная электропроводность некоторых полупроводников.

ОСНОВНЫЕ УРАВНЕНИЯ И ФОРМУЛЫ

Длина волны де Бройля: ,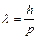

где h – постоянная Планка, р – импульс частицы.

Соотношение неопределенностей Гейзенберга для координаты и импульса: ,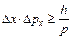

где ∆х – неопределенность координаты частицы, ∆р – неопределенность проекции импульса частицы на соответствующую координатную ось.

Соотношение неопределенностей Гейзенберга для энергии и времени: ,

где ∆E – неопределенность энергии частицы в некотором состоянии, ∆t – время нахождения частицы в этом состоянии.

Плотность вероятности нахождения частицы в соответствующем месте пространства: ,

где ψ – волновая функция частицы.

Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме: ,

где l – ширина ямы, х – координата частицы в яме (0<x<l), n – квантовое число (n=1,2,3,….).

Энергия частицы в бесконечно глубокой одномерной потенциальной яме: ,

где m – масса частицы.

Серийные формулы спектра водородоподобных атомов: ,

где λ – длина волны спектральной линии, R – постоянная Ридберга, Z – порядковый номер элемента, n=1,2,3,… k = n+1, n+2,… .

Спектральные линии характеристического рентгеновского излучения:

,

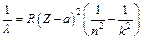где а – постоянная экранирования.

Дефект массы ядра: ,

где m_p – масса протона, m_п – масса нейтрона, m_н – масса атома водорода , m_а и m_я – масса атома и его ядра 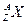, Z и А – зарядовое и массовое числа.

Энергия связи ядра: .

Удельная энергия связи: .

Закон радиоактивного распада: ,

где N₀ – начальное число радиоактивных ядер в момент времени t=0, N – число нераспавшихся радиоактивных ядер в момент времени t, λ – постоянная радиоактивного распада.

Активность радиоактивного вещества: .

Закон поглощения гамма-излучения веществом: ,

где I_о – интенсивность гамма-излучения на входе в поглощающий слой вещества, I – интенсивность гамма-излучения после прохождения поглощающего слоя вещества толщиной х, μ – линейный коэффициент поглощения.

Энергия ядерной реакции: ,

где m₁ и m₂ – массы покоя частиц, вступающих в реакцию, – сумма масс покоя частиц, образовавшихся в результате реакции.

Среднее число фононов с энергией ε_i в кристалле: ,

где k – постоянная Больцмана, Т – термодинамическая температура.

Молярная изохорная теплоемкость кристаллической решетки

при температуре Т<< θ_D: ,

при температуре Т >> θ_D: ,

θ_D – характеристическая температура Дебая.

Среднее число свободных электронов с энергией Е_i в металле: ,

где Е_F – энергия Ферми.

Примесная электропроводность полупроводников: , где е – элементарный заряд, n_ и n₊ – концентрация электронов и дырок, b_ и b₊ – подвижность электронов и дырок.