ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. 1. Кинетическая энергия протона в четыре раза меньше его энергии покоя

1. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить дебройлевскую длину волны протона.

Решение. Длина волны де Бройля λ определяется по формуле: 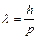. (1)

Так как по условию задачи: , (2)

то кинетическая энергия Т протона сравнима с его энергией покоя е_о, импульс р и кинетическая энергия связаны релятивистским соотношением: (3).

Подставляя в (3) условие (2), найдем: . (4)

Учитывая равенство (4), запишем (1) в виде: . (5)

Подставляя в (5) числовые значения, получим: м.

Ответ: λ =1,77·10^{-15 м.}

2. Масса движущегося электрона в три раза больше его массы покоя. Чему равна минимальная неопределенность координаты электрона?

Решение.Используя соотношению неопределенностей Гейзенбергаможно записать: 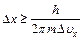.Поскольку неопределенность скорости , как и сама скорость, не может превышать скорость света с в вакууме, то: . Так как: , то получим: . Проводя вычисления, найдем: м.

Ответ: м.

3. Среднее время жизни атома в возбужденном состоянии составляет 10 нс. Вычислить естественную ширину спектральной линии (λ=0,7мкм), соответствующую переходу между возбужденными уровнями атома.

Решение. При переходе электрона из одного стационарного состояния в другое излучается (или поглощается) энергия, равная: 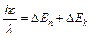, (1)

где Е_n и Е_k – энергетические уровни атома, соответствующие h– му и k– му уровням, λ – длина волны излучения. Из (1) следует, что неопределенность длины волны ∆λ излучения связана с неопределенностью энергии уровней ∆Е_n и ∆Е_k атома соотношением: . (2)

Согласно соотношению неопределенностей Гейзенберга: , где ∆t – неопределенность момента времени перехода атома из одного стационарного состояния в другое. Поскольку ∆t не превышает среднее время жизни τ возбужденного состояния атома, минимальная неопределенность энергии возбужденных уровней равна:

. (3)

Из (2) с учетом (3) найдем минимальную неопределенность длины волны излучения, которая называется естественной шириной спектральной линии: . (4)

Если одно из состояний, между которыми совершается переход, является основным, то: , поскольку для основного состояния τ = ∞. Для возбужденных состояний с одинаковым временем жизни имеем: . Подставляя числовые значения, получим: м.

Ответ: м.

4. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности.

Решение. Волновая функция ψ, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид: , где х – координата частицы в яме (0 ≤ x ≤ l). Согласно физическому смыслу волновой функции: , где w – плотность вероятности обнаружения частицы в точке с координатой х. Если частица находится на втором энергетическом уровне, то: . В соответствии с принципом соответствия Бора, выражение для классической плотности вероятности получается при n→∞: 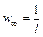. Приравниваем по условию задачи последние два выражения и получаем: . Решая это уравнение, найдем: В пределах ямы (0 ≤ x ≤ l) таких точек четыре:

Ответ:

5. Длина волны линии L_α вольфрама равна 0,148 нм. Найти постоянную экранирования.

Решение. В соответствии с законом Мозли: 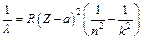, где R – постоянная Ридберга; Z – порядковый номер элемента (для вольфрама Z=74); а – постоянная экранирования; n – номер энергетического уровня, на который переходит электрон (для L-серии n=2), k – номер энергетического уровня, с которого переходит электрон (для L_α-линии k=3). Находим, что: . Подставляя числовые данные, получаем: .

Ответ: .

6. Вычислить дефект массы, энергию связи и удельную энергию связи ядра .

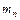Решение. Дефект массы ∆m ядра определяется по формуле: , или: . Из справочных таблиц находим: =1,00783 а.е.м., =1,00867 а.е.м., =15,99492 а.е.м. Подставляя числовые данные (для числа Z=8 и А=16), получим: а.е.м. Энергия связи ядра Е_СВ определяется по формуле: 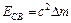. Если дефект массы ∆m выражать в а. е. м., а энергию связи в МэВ, то: . Подставляя числовые значения, получим: МэВ. Удельную энергию связи ε_СВ находим по формуле: . 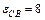Проводя вычисления, получим: МэВ.

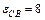Ответ: а.е.м., МэВ, МэВ.

7. Сколько атомов распадается в 1г трития за среднее время жизни этого изотопа.

Решение. Перепишем закон радиоактивного распада, учитывая, что среднее время жизни радиоактивного изотопа t находится как: , и , получим: . Число атомов, распавшихся за время , равно: . Найдем число атомов N₀ содержащихся в массе m=1 г изотопа : , где m=3∙10^-3 кг/моль – молярная масса изотопа , N_A – число Авогадро. Перепишем выражение для в виде: . Подставляя числовые значения, получим: .

Ответ: .

8. На поверхность воды падает гамма-излучение с длиной волны 0,414 пм. На какой глубине интенсивность излучения уменьшится в два раза?

Решение. Из закона поглощения гамма-излучения веществом выразим х: . Для определения коэффициента линейного ослабления вычислим энергию гамма-фотонов: 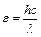. Подставляя числовые значения, получим: =3 МэВ. По графику зависимости μ от ε (рис. 4) находим, что μ=0,04 см^-1. Подставляя числовые значения в выражение для х, получим: см.

Ответ: см.

9. Вычислить энергию ядерной реакции: . Выделяется или поглощается энергия при этой реакции?

Решение. Энергия ядерной реакции определяется по формуле: . Если массу частиц выражать в а.е.м., а энергию реакции в МэВ, то формула принимает вид: . Из справочных данных находим: а.е.м., а.е.м., . Дефект массы реакции равен: а.е.м. Подставляя значение дефекта массы реакции в выражение для , получим: МэВ. Поскольку Q<0, энергия в результате реакции поглощается.

Ответ: Q=-17,3 МэВ.

10. Полоний имеет простую кубическую решетку. Постоянная решетки равна 0,334 нм. Вычислить плотность полония.

Решение. Плотность полония можно вычислить по формуле: , где m – масса атома полония, n – число атомов в единице объема. Полоний имеет простую кубическую решетку. Некоторые характеристики кубических решеток приведены в следующей таблице.

	Тип решетки
ПК	ОЦК	ГЦК
объем элементарной ячейки число атомов на одну ячейку расстояние между ближайшими соседними атомами	а3 а	а3	а3

Обозначения решеток: ПК – простая кубическая; ОЦК – объемоцентрированная кубическая; ГЦК – гранепентрированная кубическая.

Из таблицы следует, что для простой кубической решетки: , где а – постоянная решетки. Массу атома полония можно вычислить по формуле: . Получим: . Проводя вычисления, найдем: кг/м³.

Ответ: кг/м³.

11. Молярная изохорная теплоемкость аргона при температуре 4 К равна 0,174 Дж/моль∙К. Определить значение молярной изохорной теплоемкости аргона при температуре 2К.

Решение. Согласно теории Дебая, теплоемкость кристаллической решетки при низких температурах Т, когда Т<<θ_D (квантовая область), где θ_D – характеристическая температура Дебая, пропорциональна кубу термодинамической температуры: 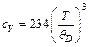. При высоких температурах, когда Т >> θ_D (классическая область), теплоемкость кристаллической решетки описывается законом Дюлонга и Пти: . Поскольку при T₁ = 4 К теплоемкость аргона много меньше, чем ЗR, выполняется закон Дебая, согласно которому: , . Отсюда: 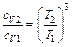или . Подставляя числовые данные, получим: Дж/моль×К.

Ответ: Дж/моль×К.

12. Дебаевская температура кристалла равна 150 К. Определить максимальную частоту колебаний кристаллической решетки. Сколько фононов такой частоты возбуждается в среднем в кристалле при температуре 300 К?

Решение.Дебаевская температура: , где – максимальная частота колебаний кристаллической решетки. Тогда: . Подставляя числовые значения, получаем: Гц. Среднее число фононов с энергией ε_i: . Энергия фонона, соответствующая частоте колебаний : . Находим: .

Ответ: Гц, .