
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. 1. Материальная точка массой 10 г совершает гармоническое колебание с периодом 1 с
1. Материальная точка массой 10 г совершает гармоническое колебание с периодом 1 с. Определить амплитуду колебаний максимальные скорость и ускорение колеблющейся точки, если полная энергия точки равна 0,02 Дж.
Решение. Уравнение гармонического колебания имеет вид:  . Скорость материальной точки определяется как первая производная от смещения по времени:
. Скорость материальной точки определяется как первая производная от смещения по времени: 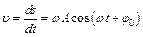 . Максимальное значение скорости равно:
. Максимальное значение скорости равно: 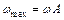 . Ускорение точки определяется как первая производная от скорости по времени:
. Ускорение точки определяется как первая производная от скорости по времени: 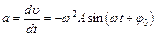 . Максимальное значение ускорения равно:
. Максимальное значение ускорения равно: 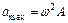 . Полная энергия колебания складывается из кинетической и потенциальной энергии и равна максимальной кинетической или максимальной потенциальной энергии:
. Полная энергия колебания складывается из кинетической и потенциальной энергии и равна максимальной кинетической или максимальной потенциальной энергии: 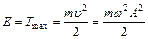 . Из этого выражения найдем амплитуду колебания:
. Из этого выражения найдем амплитуду колебания: 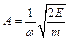 . Произведем вычисления, учитывая, что циклическая частота и период колебаний связаны соотношением:
. Произведем вычисления, учитывая, что циклическая частота и период колебаний связаны соотношением: 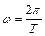 ,
, 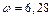 рад/с,
рад/с, 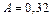 м,
м, 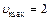 м/с,
м/с, 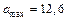 м/с2.
м/с2.
Ответ: 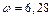 с-1,
с-1, 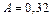 м,
м, 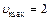 м/с,
м/с, 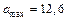 м/с2.
м/с2.
2. В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить энергию, переносимую этой волной через поверхность площадью 1 м2, расположенную перпендикулярно направлению распространения волны, за время 1 с. Период волны 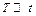 .
.
Решение. Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга: 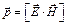 , где
, где 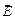 и
и 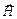 – векторы напряженности электрического и магнитного полей. Учитывая, что векторы
– векторы напряженности электрического и магнитного полей. Учитывая, что векторы 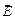 и
и 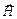 электромагнитной волны взаимно перпендикулярны, для модуля вектора
электромагнитной волны взаимно перпендикулярны, для модуля вектора 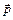 получим:
получим: 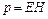 . Так как величины
. Так как величины 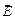 и
и 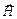 в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно:
в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно: 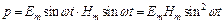 . Энергия, переносимая через площадку S, перпендикулярную направлению распространения волны, в единицу времени:
. Энергия, переносимая через площадку S, перпендикулярную направлению распространения волны, в единицу времени:  . Учитывая, что в электромагнитной волне:
. Учитывая, что в электромагнитной волне:  , найдем:
, найдем:  . Тогда выражение для
. Тогда выражение для 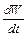 принимает вид:
принимает вид: 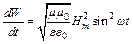 . Энергия, переносимая волной за время t, равна:
. Энергия, переносимая волной за время t, равна: 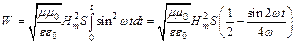 . По условию Т<<t, поэтому
. По условию Т<<t, поэтому  ; тогда:
; тогда: 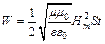 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим: 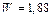 Дж.
Дж.
Ответ: 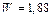 Дж.
Дж.
3. Для устранения отражения света от поверхности линзы на нее наносится тонкая пленка вещества с показателем преломления 1,25, меньшим, чем у стекла (просветление оптики). При какой наименьшей толщине пленки отражение света с длиной волны 0,72 мкм не будет наблюдаться, если угол падения лучей 60°?
Решение. Оптическая разность хода лучей, отраженных от нижней и верхней поверхности пленки, равна: 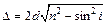 , где d– толщина пленки, n – показатель преломления пленки, i – угол падения лучей. В этом выражении учтено, что отражение лучей на обеих поверхностях происходит от оптически более плотной среды, и поэтому потери полуволны в обоих случаях компенсируют друг друга. Условие интерференционного минимума имеет вид:
, где d– толщина пленки, n – показатель преломления пленки, i – угол падения лучей. В этом выражении учтено, что отражение лучей на обеих поверхностях происходит от оптически более плотной среды, и поэтому потери полуволны в обоих случаях компенсируют друг друга. Условие интерференционного минимума имеет вид: 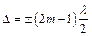 ,
,  Тогда:
Тогда: 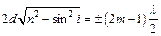 . Из этого выражения найдем возможные значения толщины пленки:
. Из этого выражения найдем возможные значения толщины пленки: 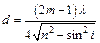 . Наименьшее значение толщины пленки будет при m = 1:
. Наименьшее значение толщины пленки будет при m = 1:  . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим: 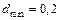 мкм.
мкм.
Ответ: 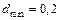 мкм.
мкм.
4. Постоянная дифракционной решетки 10 мкм, ее ширина 2 см. В спектре какого порядка эта решетка может разрешить дублет λ1 = 486,0 нм и λ2 = 486,1 нм?
Решение. Разрешающая способность дифракционной решетки: 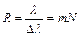 , где ∆λ – минимальная разность длин волн двух спектральных линий λ и λ+∆λ, разрешаемых решеткой; m – порядок спектра; N – число щелей решетки. Поскольку постоянная решетки d есть расстояние между серединами соседних щелей, общее число щелей можно найти как:
, где ∆λ – минимальная разность длин волн двух спектральных линий λ и λ+∆λ, разрешаемых решеткой; m – порядок спектра; N – число щелей решетки. Поскольку постоянная решетки d есть расстояние между серединами соседних щелей, общее число щелей можно найти как:  , где l – ширина решетки. Тогда:
, где l – ширина решетки. Тогда: 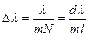 . Дублет спектральных линий λ1 и λ2 будет разрешен, если:
. Дублет спектральных линий λ1 и λ2 будет разрешен, если: 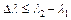 . Используя поледние выражения и учитывая, что λ = λ1 , получим:
. Используя поледние выражения и учитывая, что λ = λ1 , получим: 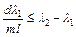 . Подставляя числовые данные, получим:
. Подставляя числовые данные, получим: 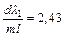 . Так как m целое число, то m
. Так как m целое число, то m  3.
3.
Ответ: m  3.
3.
5. Естественный свет падает на поверхность диэлектрика под углом полной поляризации. Степень поляризации преломленного луча составляет 0,124. Найти коэффициент пропускания света.
Решение. Естественный свет можно представить как наложение двух некогерентных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность: 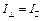 , где индексы
, где индексы 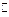 и
и 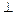 обозначают колебания, параллельные и перпендикулярные плоскости падения света на поверхность диэлектрика, причем интенсивность падающего света:
обозначают колебания, параллельные и перпендикулярные плоскости падения света на поверхность диэлектрика, причем интенсивность падающего света: 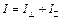 . При падении света под углом полной поляризации отражаются только волны, поляризованные в плоскости, перпендикулярной плоскости падения. В преломленной волне преобладают колебания, параллельные плоскости падения. Интенсивность преломленной волны можно записать как:
. При падении света под углом полной поляризации отражаются только волны, поляризованные в плоскости, перпендикулярной плоскости падения. В преломленной волне преобладают колебания, параллельные плоскости падения. Интенсивность преломленной волны можно записать как: 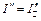 . Составляющие
. Составляющие 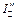 и
и 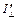 интенсивности преломленной волны равны:
интенсивности преломленной волны равны:  и
и 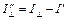 , где
, где 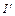 – интенсивность отраженного света. Степень поляризации преломленного луча:
– интенсивность отраженного света. Степень поляризации преломленного луча:  . Выражение для
. Выражение для 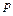 можно представить в виде:
можно представить в виде: 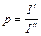 . Коэффициент пропускания света:
. Коэффициент пропускания света:  или
или  . Проводя вычисления, получим:
. Проводя вычисления, получим: 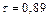 .
.
Ответ: 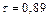 .
.
6. Интенсивность естественного света, прошедшего через поляризатор, уменьшилась в 2,3 раза. Во сколько раз она уменьшится, если за первым поставить второй такой же поляризатор так, чтобы угол между их главными плоскостями был равен 60°?
Решение. Естественный свет можно представить как наложение двух некогерентных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность. Идеальный поляризатор пропускает колебания, параллельные его главной плоскости, и полностью задерживает колебания, перпендикулярные этой плоскости. На выходе из первого поляризатора получается плоскополяризованный свет, интенсивность которого 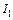 с учетом потерь на отражение и поглощение света поляризатором равна:
с учетом потерь на отражение и поглощение света поляризатором равна: 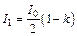 , где
, где 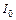 – интенсивность естественного света; k – коэффициент, учитывающий потери на отражение и поглощение После прохождения второго поляризатора интенсивность света уменьшается как за счет отражения и поглощения света поляризатором, так и из-за несовпадения плоскости поляризации света с главной плоскостью поляризатора. В соответствии с законом Малюса, учитывая потери на отражение и поглощение света, имеем:
– интенсивность естественного света; k – коэффициент, учитывающий потери на отражение и поглощение После прохождения второго поляризатора интенсивность света уменьшается как за счет отражения и поглощения света поляризатором, так и из-за несовпадения плоскости поляризации света с главной плоскостью поляризатора. В соответствии с законом Малюса, учитывая потери на отражение и поглощение света, имеем: 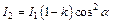 , где
, где 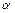 – угол между плоскостью поляризации света, которая параллельна главной плоскости первого поляризатора, и главной плоскостью второго поляризатора. Найдем, во сколько раз уменьшилась интенсивность света:
– угол между плоскостью поляризации света, которая параллельна главной плоскости первого поляризатора, и главной плоскостью второго поляризатора. Найдем, во сколько раз уменьшилась интенсивность света: 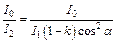 . Из первой формулы имеем:
. Из первой формулы имеем: 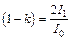 , и
, и 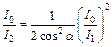 . Проведя вычисления, найдем:
. Проведя вычисления, найдем: 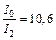 .
.
Ответ: 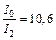 .
.
7. Измерение дисперсии показателя преломления оптического стекла дало n1 = 1,528 для 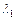 – 0,434 мкм и n2 = 1,523 для
– 0,434 мкм и n2 = 1,523 для 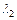 = 0,486 мкм. Вычислить отношение групповой скорости к фазовой для света с длиной волны 0,434 мкм.
= 0,486 мкм. Вычислить отношение групповой скорости к фазовой для света с длиной волны 0,434 мкм.
Решение. Зависимость групповой скорости и от показателя преломления n и длины волны  имеет вид:
имеет вид:  . Фазовая скорость определяется как:
. Фазовая скорость определяется как:  . Получим отношение
. Получим отношение 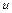 к
к 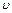 :
: 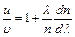 . Для длины волны
. Для длины волны 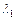 и средней дисперсии
и средней дисперсии 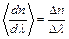 имеем:
имеем: 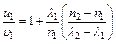 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим: 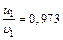 .
.
Ответ: 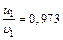 .
.
8. В черенковском счетчике из каменной соли релятивистские протоны излучают в конусе с раствором 82°. Определить кинетическую энергию протонов. Показатель преломления каменной соли 1,54.
Решение. Излучение Вавилова–Черенкова возникает, когда скорость движения 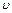 заряженной частицы в среде больше фазовой скорости света с/n в этой среде. Излучение направлено вдоль образующих конуса, ось которого совпадает с направлением движения частицы. Угол θ между направлением излучения и направлением движения частицы определяется формулой:
заряженной частицы в среде больше фазовой скорости света с/n в этой среде. Излучение направлено вдоль образующих конуса, ось которого совпадает с направлением движения частицы. Угол θ между направлением излучения и направлением движения частицы определяется формулой: 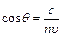 . Кинетическая энергия релятивистской частицы определяется как:
. Кинетическая энергия релятивистской частицы определяется как: 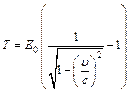 , где
, где 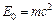 энергия покоя частицы; m0 – масса покоя. Для протонов E0 = 989 МэВ. Отношение определим как:
энергия покоя частицы; m0 – масса покоя. Для протонов E0 = 989 МэВ. Отношение определим как:  . Кинетическая энергия определится как:
. Кинетическая энергия определится как: 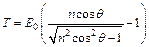 . Проводя вычисления, найдем:
. Проводя вычисления, найдем: 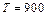 МэВ.
МэВ.
Ответ: 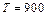 МэВ.
МэВ.
9. Во сколько раз увеличится мощность излучения черного тела, если максимум энергии излучения сместится от красной границы видимого спектра к его фиолетовой границе?
Решение. Длина волны 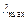 , на которую приходится максимум энергии излучения черного тела, согласно закону смещения Вина, равна:
, на которую приходится максимум энергии излучения черного тела, согласно закону смещения Вина, равна: 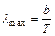 , где Т – термодинамическая температура тела; b – постоянная Вина. Определяем температуру, при которой максимум энергии излучения приходится на красную
, где Т – термодинамическая температура тела; b – постоянная Вина. Определяем температуру, при которой максимум энергии излучения приходится на красную 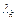 , и фиолетовую
, и фиолетовую 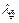 границы видимого спектра:
границы видимого спектра: 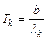 и
и 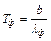 . Мощность излучения равна:
. Мощность излучения равна:  , где R – энергетическая светимость тела; S – площадь его поверхности. В соответствии с законом Стефана - Больцмана:
, где R – энергетическая светимость тела; S – площадь его поверхности. В соответствии с законом Стефана - Больцмана: 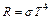 , где
, где 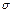 – постоянная Стефана–Больцмана. Для температур Tк и Тф имеем:
– постоянная Стефана–Больцмана. Для температур Tк и Тф имеем: 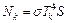 и
и 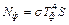 . Тогда:
. Тогда:  или
или 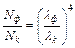 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим:  .
.
Ответ:  .
.
10. Давление света с длиной волны 0,55 мкм нормально падающего на зеркальную поверхность равно 9 мкПа. Определить концентрацию фотонов вблизи поверхности.
Решение. Давление света при нормальном падении на поверхность с коэффициентом отражения 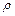 определяется по формуле:
определяется по формуле:  , где
, где  – интенсивность света; с – скорость света в вакууме; w – объемная плотность энергии излучения,
– интенсивность света; с – скорость света в вакууме; w – объемная плотность энергии излучения, 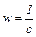 . Объемная плотность энергии w равна произведению концентрации фотонов n (числа фотонов в единице объема) на энергию одного фотона
. Объемная плотность энергии w равна произведению концентрации фотонов n (числа фотонов в единице объема) на энергию одного фотона 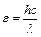 , т. е.:
, т. е.: 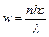 , где h – постоянная Планка; λ – длина волны света. Выражение для давления света преобразуется как:
, где h – постоянная Планка; λ – длина волны света. Выражение для давления света преобразуется как: 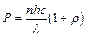 , откуда:
, откуда: 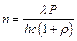 . Проводя вычисления, найдем:
. Проводя вычисления, найдем: 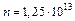 м-3.
м-3.
Ответ: 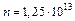 м-3.
м-3.
11. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5 В.
Решение. Согласно уравнению Эйнштейна для внешнего фотоэффекта:  , где h – постоянная Планка; λ – длина волны света; А – работа выхода электронов из металла; Tmax – максимальная кинетическая энергия фотоэлектронов. Красная граница фотоэффекта определяется из условия равенства энергии фотона работе выхода электронов, т. е.:
, где h – постоянная Планка; λ – длина волны света; А – работа выхода электронов из металла; Tmax – максимальная кинетическая энергия фотоэлектронов. Красная граница фотоэффекта определяется из условия равенства энергии фотона работе выхода электронов, т. е.: 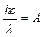 . Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов U:
. Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов U: 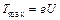 , где е – заряд электрона. Тогда:
, где е – заряд электрона. Тогда:  . Найдем длину волны света:
. Найдем длину волны света: 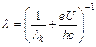 . Подставляя числовые значения, получим:
. Подставляя числовые значения, получим: 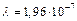 м.
м.
Ответ: 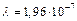 м.
м.
12. Гамма-фотон с длиной волны 1,2 пм в результате комптоновского рассеяния на свободном электроне отклонился от первоначального направления на угол 60°. Определить кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился.
Решение. Изменение длины волны фотона при комптоновском рассеянии на неподвижном свободном электроне равно: 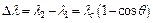 , где λ1 и λ2 – длины волн падающего и рассеянного фотона; θ – угол рассеяния фотона;
, где λ1 и λ2 – длины волн падающего и рассеянного фотона; θ – угол рассеяния фотона; 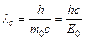 – комптоновская длина волны электрона. Найдем длину волны рассеянного фотона:
– комптоновская длина волны электрона. Найдем длину волны рассеянного фотона: 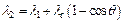 . Выразим энергию падающего и рассеянного фотона через его длину волны:
. Выразим энергию падающего и рассеянного фотона через его длину волны: 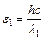 и
и 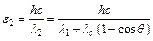 . Кинетическая энергия электрона отдачи согласно закону сохранения энергии равна:
. Кинетическая энергия электрона отдачи согласно закону сохранения энергии равна: 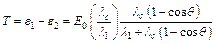 . Проводя вычисления, получим:
. Проводя вычисления, получим: 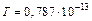 Дж. Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя, импульс и кинетическая энергия связаны релятивистским соотношением:
Дж. Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя, импульс и кинетическая энергия связаны релятивистским соотношением:  . Подставляя числовые данные, получим:
. Подставляя числовые данные, получим: 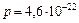 кг∙м/с.
кг∙м/с.
Ответ: 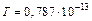 Дж,
Дж, 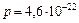 кг∙м/с.
кг∙м/с.
Дата добавления: 2014-10-31; просмотров: 1248; Мы поможем в написании вашей работы!; Нарушение авторских прав |