Логико-вероятностный метод расчета надежности сложных систем

Метод основан на математическом аппарате алгебры логики. Расчет надежности системы управления предполагает определение связи между сложным событием (отказ системы) и событиями, от которых оно зависит (отказы элементов системы). Следовательно, расчеты на надежность основаны на проведении операций с событиями и высказываниями, в качестве которых принимаются утверждения о работоспособности или отказе элемента (системы). Каждый элемент системы представляется логической переменной, принимающей значение 1 или 0.

События и высказывания при помощи операций дизъюнкции, конъюнкции и отрицания объединяются в логические уравнения, соответствующие условию работоспособности системы. Составляется логическая функция работоспособности. Расчет, основанный на непосредственном использовании логических уравнений, называется логико-вероятностным и выполняется в семь этапов:

1. Словесная формулировка условий работоспособности объекта. Описывается зависимость работоспособности информационной системы от состояния ее отдельных элементов.

2. Составление логической функции работоспособности. Представляет собой логическое уравнение, соответствующее условию работоспособности системы управления

которое выражено в дизъюнктивной форме, например:

,

где x_i – условие работоспособности i-го элемента Fл; X_i = 1 – работоспособное состояние, X_i = 0 – неработоспособное состояние.

3. Приведение логической функции работоспособности F_Л к ортогональной бесповторной форме F_ЛО. Сложную логическую функцию работоспособности необходимо привести к ортогональной бесповторной форме.

Функция вида (2.2) называется ортогональной, если все ее члены D_i попарно ортогональны (то есть, их произведение равно нулю), и бесповторной, если каждый ее член D_i состоит из букв х_i, с разными номерами (то есть отсутствуют повторяющиеся аргументы), например: произведение элементарных конъюнкций х₁, х₂, x₄ и х₃, x₂ равно нулю, так как одна из них содержит x₂, а другая – x₂, следовательно, они ортогональны; D₁ = x₁×x₂×x₂, где x₂ и x₂ имеют один и тот же номер, поэтому член D₁ не является бесповторным.

– ортогональная бесповторная форма;

– ортогональная, но не бесповторная форма.

Функцию F_л можно преобразовать к ортогональной бесповторной форме F_ло, используя законы и правила преобразования сложных высказываний. При расчетах наиболее употребительны правила:

4. Арифметизация F_ло. По найденной ортогональной бесповторной логической функции работоспособности F_ЛО определяется арифметическая функция F_a (2.3).

где A_i – арифметическая форма членов D_i функции F_ло.

Арифметизация членов D_i, в общем виде содержащих операции дизъюнкции, конъюнкции и отрицания, осуществляется заменой логических операций арифметическими по правилам:

5. Определение вероятности безотказной работы системы.

Вероятность безотказной работы системы устанавливается как вероятность истинности логической функции работоспособности, представленной в ортогональной бесповторной форме, и вычисляется как сумма вероятностей истинности всех ортогональных членов этой функции алгебры логики. Все события (высказывания) заменяются их вероятностями (вероятностями безотказной работы соответствующих элементов).

6. Вычисление требуемых показателей надежности системы управления по найденному показателю P_c(t):

-вероятность безотказной работы P_c(t);

-вероятность отказа Q_c(t) = 1 – P_c(t);

-интенсивность отказов

;

-средняя наработка до отказа ;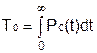

7. Анализ соответствия полученных показателей надежности заданным техническим требованиям системы.

Допущения, принимаемые при логико-вероятностном методе: для элементов системы возможны только два состояния; метод применим для невосстанавливаемых систем; отказы элементов системы должны быть независимы.