Методика определения показателей надежности при использовании топологического метода

Теперь рассмотрим методику расчета показателей надежности топологическим методом в установившемся режиме, где топологические коэффициенты С_i для каждой x_i вершины графа определяются непосредственно по графу, а затем вычисляется нужный показатель по ниже приведенным топологическим формулам.

Для определения коэффициента С_i необходимо:

- выбрать начальную вершину графа x_q отдельно для определения каждого из коэффициентов С_i

начальная вершина может быть выбрана произвольно, однако выбор влияет на объем вычислений, поэтому ее надо выбирать так, чтобы были длинные прямые пути;

– построить множество К прямых путей из начальной вершины x_q в вершину x_i, для которой определяется коэффициент;

– для каждого k-го прямого пути построить множество замкнутых контуров подграфа G{X_k} и образовать возможные комбинации независимых замкнутых контуров (множество соединений S), где G{X_k} – подграф графа G{X, W}, образованный удалением множества вершин, входящих в k-й путь и прилегающих к нему дуг;

– записать коэффициенты C_i по найденным составляющим по формуле

гдe К – множество прямых путей из произвольно выбранной вершины х_q в х_i; Х_к - множество вершин, входящих в k-ый прямой путь.

Используя топологические коэффициенты, основные показатели надежности установившегося режима можно записать:

– вероятность нахождения системы в i-м состоянии

где n – число вершин графа;

– коэффициент готовности

где I_p – множество индексов работоспособных состояний системы;

– коэффициент простоя

где J – множество индексов неработоспособных состояний системы;

– среднюю наработку на отказ

где

– подмножество индексов граничных состояний из X_р, из которых в неработоспособное состояние можно попасть за один переход;

– среднее время восстановления

где J⁺ – подмножество индексов граничных состояний из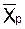

из которых в работоспособное состояние можно попасть за один переход.

Основные положения топологического метода могут быть применены для определения показателей надежности неустановившегося режима с использованием преобразований Лапласа.