
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Показатели безотказности невосстанавливаемых систем. В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса)
В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t), которая в данном случае будет называться функцией вероятности отказа Q(t), т.е.:
 .
.
Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t:
 .
.
Графики, дающие представление о характерах изменения функций P(t) и Q(t), представлены на рисунке:

Плотность распределения вероятностей как показатель безотказности невосстанавливаемых систем принимает смысл плотности распределения наработки на отказ fH(t), а интенсивность b(t) принимает смысл функции интенсивности отказов l(t):
 .
.
 .
.
Между функциями P(t) и l(t) существует взаимосвязь:  .
.
Взаимосвязь между функциями fH(t) и l(t) можно определить из соотношения:
 .
.
Если одна из четырех функций известна, то остальные три можно вычислить по формулам, приведенным в таблице.
Удобный и наглядный физический смысл имеет показатель "средняя наработка на отказ", который равен математическому ожиданию времени исправной работы до первого отказа:
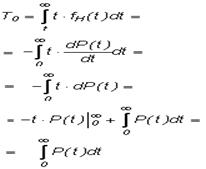
Свойства функции безотказной работы P(t):
1.При t=0, P(t)=1 , т.е. в нулевой момент времени система будет работоспособна.
2. P(t) — монотонно убывающая функция во времени.
3.При t→∞, P(t) → 0.
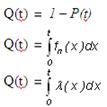



Дата добавления: 2015-01-19; просмотров: 236; Мы поможем в написании вашей работы!; Нарушение авторских прав |