Количественные показатели надежности как характеристики случайных величин

Рассмотрим количественные показатели случайных величин, которые могут характеризовать свойства безотказности, ремонтопригодности, сохраняемости и долговечности. В качестве единиц измерения применяются:

- для безотказности - непрерывное время безотказной работы системы (наработка на отказ T’);

- для долговечности - время от момента изготовления системы до предельного состояния или списания. (срок службы T’’);

- для ремонтнопригодности - время восстановления работоспособности T’’’;

- для сохраняемости - случайное время сохранения работоспособности в состоянии хранения “T”.

Случайные величины, позволяют количественно оценить путем применения математического аппарата теории вероятностей и математической статистики. Полной характеристикой любой случайной величины является закон ее распределения, используемый в двух видах: как функция распределения (интегральный закон) и как плотность распределения (дифференциальный закон).

Функцией распределения называется функция F(t), определяющая вероятность того, что случайная величина Т примет значение, меньшее заданной величины t, т.е.: .

Плотностью распределения вероятностей непрерывной случайной величины Т в диапазоне от 0 до бесконечности называют функцию f(t) - первую производную от функции распределения F(t):

.

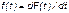В теории надежности широко используются еще две функции:

обратная функция распределения: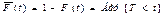

интенсивность:

Рассмотрим графики этих функций.(рис. 1.3-1.6).

Рис.1.3. График функции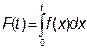

Рис.1.4. График функции

Рис. 1.4. График функции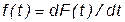

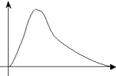
Рис.1.5. График функции

Зависимость между функциями 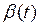и можно определить из соотношений: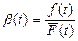

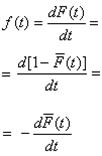
Подставим выражение (1.2.6) в (1.2.5):

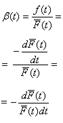
Проинтегрируем обе части выражения:

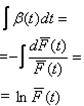
Таким образом, получаем зависимость