
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 1. КИНЕМАТИКА
Смугами рівного нахилу наз. диференціальна картина, яка утворюється при падінні світла на паралельну площину фіксованої товщини під однаковими кутами.
Смуги рівного нахилу локалізовані та нескінченні 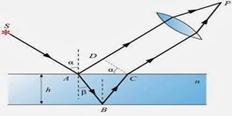
Смуги рівної товщини.
Допустимо, що товщина пластинки не постійна (∼b, n = const).
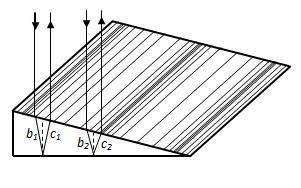 Тоді у всіх тих місцях пластинки, де товщина b, а отже, і різниця ходу Δ однакові, спостерігається той самий результат інтерференції. Це означає, що уздовж якої-небудь темної або світлої інтерференційної смуги, що утворюється на поверхні, товщина цієї пластинки та сама.
Тоді у всіх тих місцях пластинки, де товщина b, а отже, і різниця ходу Δ однакові, спостерігається той самий результат інтерференції. Це означає, що уздовж якої-небудь темної або світлої інтерференційної смуги, що утворюється на поверхні, товщина цієї пластинки та сама.
Смуги рівної товщини локалізовані на поверхні пластинки. При спостереженні в білому світлі смуги будуть пофарбовані так, що поверхня містить усі кольори веселки. Приклад смуг рівної товщини: нафтові плями, мильні плівки і т.д.
Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщиниb, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою. Нехай показник заломлення зазору n, товщина в точці Е рівна b. Паралельний пучок світла падає нормально (i1= 0°) на плоску поверхню ВС лінзи й відбивається від верхньої й нижньої поверхні зазору ( від т. Е і F ).
Білет 17
1.Коливання називаються вільними, якщо вони здійснюються за рахунок енергії, яка була надана, за відсутності в наступному зовнішніх впливів на коливну систему.
гармонічні коливання – коливання, при яких значення фізичної величини змінюється з часом за законом косинуса (синуса)
Нехай матеріальна точка здійснює прямолінійні гармонічні коливання вздовж осі координат 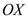 біля положення рівноваги, яке прийняте за початок координат. Тоді залежність координатих від часу
біля положення рівноваги, яке прийняте за початок координат. Тоді залежність координатих від часу 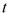 задається рівнянням
задається рівнянням
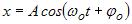 .
.
Тут 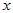 – зміщення коливної точки;
– зміщення коливної точки; 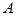 – амплітуда коливання
– амплітуда коливання  ;
; 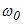 – циклічна частота;
– циклічна частота; 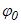 – початкова фаза коливань в момент часу
– початкова фаза коливань в момент часу 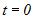 ;
;  – фаза коливань в момент часу
– фаза коливань в момент часу 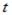 .
.
Найменший проміжок часу Т, після проходження якого повторюються значення всіх фізичних величин, що характеризують коливання, називається періодом коливання. За час Тздійснюється одне повне коливання і фаза коливань отримує приріст 
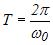 ., Частотою коливань називається кількість повних коливань, що здійснюються за одиницю часу:
., Частотою коливань називається кількість повних коливань, що здійснюються за одиницю часу:
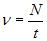
Циклічна частота

2. Ті точки середовища, у яких амплітуда стоячої хвилі максимальна й рівна 2А, називаються пучностями. Координати пучностей можна знайти з умови, що
 звідси
звідси 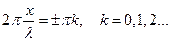 ,,,,
,,,, 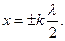
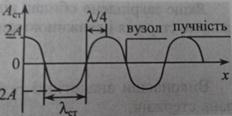
Відстань між двома сусідніми пучностями рівна о 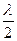 .
.
Точки, у яких амплітуда стоячої хвилі мінімальна й рівна 0, називаються вузлами. Координата вузлів можна знайти з умови
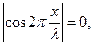 звідси
звідси 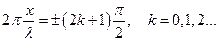 ,,,,,,
,,,,,, 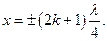
3.Кільця Ньютона - приклад смуг рівної товщини. Вони спостерігаються при відбитті світла. від дотичних одна з одною плоско паралельної товстої скляної пластинки й плоско опуклої лінзи з великим радіусом кривизни. Роль тонкої плівки змінної товщини b, від поверхні якої відбиваються когерентні хвилі, відіграє зазор між пластинкою й лінзою. Нехай показник заломлення зазору n, товщина в точці Е рівна b. Паралельний пучок світла падає нормально (i1= 0°) на плоску поверхню ВС лінзи й відбивається від верхньої й нижньої поверхні зазору ( від т. Е і F ).
Оптична різниця ходу між променями, відбитими від верхньої й нижньої поверхні зазору рівна
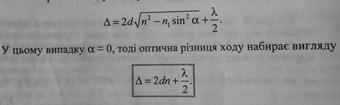
Білет 18
1. Гармонічні коливання – періодичні коливання, які з часом змінюються за гармонічним законом та повертаючи сила змінюються за квазіупружним законом.
Диф. Р-ння
F=Fпов
За 2 законом Ньютона: ma = -kx
ma+kx = 0
md2x/dt2 + kx = 0
d2t/dt2 + ɷ02x = 0 де ɷ — циклічна частота, k — хвильове число.
2. Фазова швидкість — одна із характеристик хвилі, що характеризує поширення збурення будь якої фізичної природи. Поняття фазової швидкості може використовуватись при розповсюдженні збурень будь якої форми, якщо в впроцесі розповсюдження ця форма не змінюється. На рисунку проілюстровано визначення фазової швидкості збурень в струні.
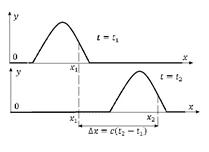
V = √E/ρ V=√G/ρ
Групова швидкість хвиль - швидкість руху групи або низки хвиль, яка за відсутності поглинання в середовищі збігається із швидкістю переміщення енергії цієї групи хвиль.
U = υ – λ* (dυ/dλ)
3. Когереними назив світлові хвилі з однаковою частотою, сталою різницею фаз та для яких коливання векторів напруженостей електричного і магнітного полів відбувається у взаємно перпендикулярних площинах, тобто є впорядкованими.
max: Δ= ±2 k* λ/2 min: Δ= ±(2 k+1)* λ/2
Інтерференцією світла назив. Явище накладання двох або кількох когерентних світлових хвили, в результаті якого відбувається перерозподіл інтенсивності в просторі.
max: Δᵠ = ±2 kπ min: Δᵠ = ±(2 k +1)π
Лекция 1. КИНЕМАТИКА
Предмет кинематики; радиус-вектор и перемещение; скорость; ускорение;
обратная задача кинематики; движение по окружности


|
1. Предмет кинематики
Механика— раздел физики, где изучается
простейший вид движения материи —
механическое движение тел в пространстве и во
времени.
Движение тел в механике рассматривается
относительно выбранной системы отсчета.
Система отсчета(СО) — это тело, условно
считающееся неподвижным, относительно
которого рассматривается движение исследуемого
тела, плюс часы, по которым отсчйтывается время.
С выбранным в качестве СО телом жестко
связана система координат (чаще всего
прямоугольная декартова система XYZ).
В механике важную . роль играют два
абстрактных идеальных понятия: материальная
точка (частица) и абсолютно твердое тело.
Материальная точка— это тело, размерами
которого можно пренебречь в условиях данной
конкретной задачи. Абсолютно твердое тело—
это тело, форма и размеры которого не меняются
под воздействием других тел. Абсолютно твердое
тело можно рассматривать как совокупность
жестко связанных между собой материальных
точек, т.е. как систему материальных точек,
расстояния между которыми не изменяются в
процессе движения тела.
Если движение тел происходит со скоростями,
значительно меньшими скорости света в вакууме
с = 3108 м/с (движение ракет, спутников, планет
и т.д.), то такое движение с практически
стопроцентной точностью описывается
нерелятивистской ньютоновской механикой,
основные законы которой были сформулированы
еще Ньютоном.
Законы Ньютона перестают работать, когда
скорость тела становится сравнимой со скоростью
света (например, при движении частиц в
современных ускорителях заряженных частиц). В
этом случае движение материальной точки
описывается релятивистской механикой
Эйнштейна. Следует помнить, что ньютоновская
механика вытекает из релятивистской при
скоростях v « с. В этом семестре мы будем
изучать основные законы ньютоновской механики
применительно к движению материальных точек
и абсолютно твердого тела и попытаемся усвоить
основные положения механики Эйнштейна.
Позже мы узнаем, что механика Ньютона
оказывается бессильной и при рассмотрении
движения микрочастиц в областях, размеры
которых ~10~10 м (движение электрона в атоме).
Такое движение подчиняется законам
квантовой механики, которые Вы узнаете в
третьем семестре.
Изучение механики Ньютона мы начинаем с
кинематикиматериальной точки — раздела
механики, в котором рассматривается движение
материальной точки без выяснения причин,
вызывающих то или иное ее движение.
2. Радиус-вектор и перемещение
Положение материальной точки (частицы) в
пространстве в данный момент времени t
однозначно определяется в выбранной СО
заданием ее трех координат. Поэтому и говорят,
что частица обладает тремя степенями свободы.
Вообще говоря, число степеней свободы— это
минимальное число независимых координат, с
помощью которых можно однозначно определить
положение тела в пространстве. Так, например,
ясно, что положение в пространстве абсолютно
твердого тела произвольной формы нельзя
однозначно задать лишь с помощью трех
координат. Обычно поступают следующим
образом. С твердым телом связывают систему
координат O'X'Y'Z', и положение тела в
пространстве в неподвижной системе координат
OXYZ определяют заданием трех координат х0, Уо(
z0 начала отсчета О' системы, связанной с телом, и
трех углов а, Р, у между осями ОХ и О'Х', OY и
O'Y', OZ и O'Z'. Следовательно, абсолютно твердое
тело произвольной формы обладает шестью
степенями свободы.
Положение материальной точки в
пространстве удобно задавать не только ее тремя
координатами х, у, z, но и ее радиус-вектором—
вектором г , проведенным из начала координат к
материальной точке. Ясно, что проекции радиус-
вектора на оси OX, OY, OZ совпадают с
координатами частицы х, у, z, т.е.
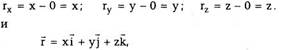
где i, j,k — единичные векторы (орты) вдоль осей
OX, OY, OZ.
При движении материальной точки ее
координаты изменяются со временем, а конец
радиус-вектора описывает в пространстве
некоторую линию, которая называется
траекторией.
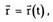
|
| которой эквивалентны три уравнения: x = x(t); y = y(t); z = z(t). (1.1) |
Уравнением траектории в векторной форме
называется зависимость радиус-вектора г
материальной точки от времени:
Для получения уравнения траектории частицы
в явном виде из системы (1.1) необходимо
исключить время t. Если при своем движении
материальная точка находится все время в одной
плоскости, то такое движение называется
плоским.
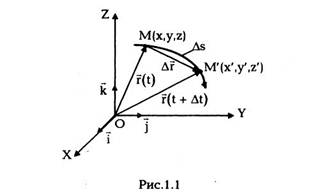
Пусть за время At частица переместилась из
точки М(х, у, z), где она находилась в момент
времени t, в точку М'(х', у', z'), пройдя вдоль
траектории отрезок пути As (рис. 1.1).
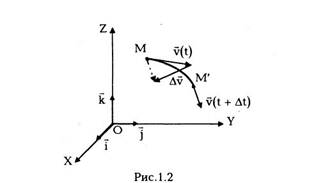
Вектор скорости(мгновенной) материальной
точки v(t) в данный момент времени t
определяется как предел, к которому стремится
вектор средней скорости (v) за время от t до
t + At при безграничном уменьшении промежутка
времени At:
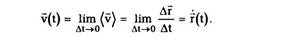
|

|
Здесь точка сверху означает производную по
времени, которую принято записывать в виде:

где dr = dxi + dyj + dzk — бесконечно малый
вектор перемещения частицы за бесконечно
малый промежуток времени dt. Заметим, что при
At -» О вектор Аг -> dr и направлен по
касательной к траектории частицы в момент
времени t в сторону движения, а по абсолютной
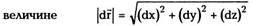
не

|

|
отличается от бесконечно малого отрезка пути
частицы ds за время dt, т.е. |dr| = ds. Итак,
Таким образом, вектор скорости частиц v(t)
направлен по касательной к траектории в момент
времени t в сторону движения, его проекции на
оси OX, OY, OZ определяются соотношениями
(1.26), а абсолютная величина — соотношением
(1.3).
4. Ускорение
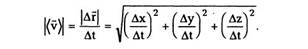
|

|

|

|

|

|

|
|

|

|

|

|

|
Вектор ускорениячастицы a(t) в момент
времени t определяется как предел отношения Av
к At при At->0:
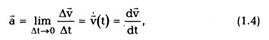
где dv — бесконечно малое изменение вектора
скорости за бесконечно малый промежуток
времени dt. Выражение (1.4) можно записать в
виде:
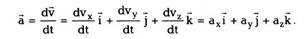
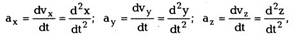
|
| а модуль вектора ускорения |
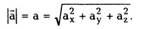
|
Следовательно, проекции вектора ускорения
на координатные оси (с учетом (1.2))
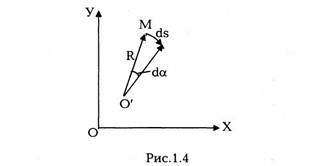
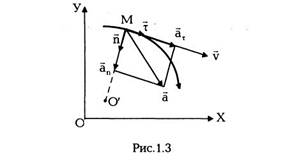
Если движение материальной точки плоское
(будем в дальнейшем считать, что траектория
частицы лежит в плоскости ХОУ), то вектор
ускорения а всегда можно разложить на две
взаимно перпендикулярные составляющие (см.
рис. 1.3):
б

|
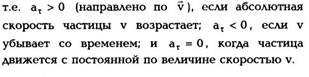
|
При равноускоренном движении
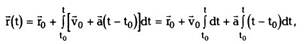
Откуда
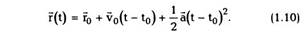
Дата добавления: 2014-10-31; просмотров: 381; Мы поможем в написании вашей работы!; Нарушение авторских прав |