
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 4. РАБОТА И ЭНЕРГИЯ
Работа постоянной и переменной силы; теорема о кинетической энергии;
потенциальные силы; потенциальная энергия; закон сохранения энергии.
 1. Работа постоянной и переменной
1. Работа постоянной и переменной
силы
Из школьного курса физики мы знаем, что при
движении частицы по прямолинейной траектории
постоянная по величине и направлению сила
f совершает над частицей работу

где f — модуль силы, As — отрезок
прямолинейного пути и а — угол между
направлениями силы и перемещения. Выражение
(4.1) можно записать в виде

Интеграл в правой части (4.3) называется
криволинейным интегралом 1-го рода.Из (4.3)
следует, что при движении частицы из точки 2 в
точку 1 по той же самой траектории работа силы
f :

Вспомним теперь, что ds = |dr|, где dr —
вектор бесконечно малого перемещения. Тогда

где fs — проекция силы на перемещение. Из
определения работы видно, что последняя может
быть как положительной, когда fs>0, так и
отрицательной, когда fs<0, и равной нулю, когда
сила перпендикулярна перемещению.
Спрашивается, как найти работу силы f ,
которая в разных точках траектории движения
различна по величине и направлению (говорят,
что частица движется в неоднородном силовом
поле f(x,y,z))r а сама траектория криволинейна
(см. рис.4.1).

Поступают следующим образом. Всю
траекторию от начальной точки 1 до конечной 2
разбивают на бесконечно малые участки ds,
которые в силу своей бесконечной малости можно
считать прямолинейными. Опять же в силу того,
что путь ds бесконечно малый, можно считать, что
сила f остается постоянной как по величине, так и
по направлению на этом участке пути ds. Тогда,
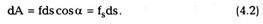
|
| Работа же силы f на конечном участке траектории от начальной точки 1 до конечной 2 |
согласно (4.1), элементарная работа силы f на
пути ds

Последний интеграл называется
Дата добавления: 2014-10-31; просмотров: 345; Мы поможем в написании вашей работы!; Нарушение авторских прав |