Теорема о кинетической энергии

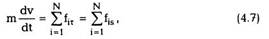
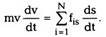
Пусть частица массой m движется из точки 1 в
точку 2 по криволинейной траектории под

Сокращая на dt и преобразуя левую часть

Интегрируя теперь (4.8) от начальной точки 1
до конечной 2, получим окончательно:

где v_{ — скорость тела в начале и v₂ — в конце.
Выражение

называется кинетической энергией

материальной точки,а (4.9) — теоремой о
кинетической энергии:приращение

в точку 2 вдоль кривой а, а затем из точки 2 назад
в точку 1 вдоль кривой Ь. Общая работа, которая
производится при этом консервативной силой

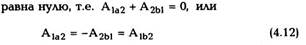
т.е. работа не зависит от вида кривой,
соединяющей начальную и конечную точки 1 и 2.
Этот факт свидетельствует о том, что работа
консервативной силы является величиной,
имеющей глубокое физическое содержание.

Дата добавления: 2014-10-31; просмотров: 30; Нарушение авторских прав