
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Силы упругости.
Эти силы возникают в твердом теле при его
деформировании (изменении его формы).
Простейшим видом деформации тела является его
растяжение или сжатие. Например, оно возникает
в тонком стержне, один конец которого
закреплен, а к другому приложена сила f
перпендикулярно основанию стержня. Упругое
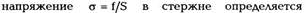
величиной силы f, отнесенной к площади
поперечного сечения стержня S. Это напряжение
одинаково вдоль всей длины стержня. Если
приложенная сила i не очень велика и можно
пренебречь изменением толщины стержня, то
справедлив закон Гука:

где 6L — удлинение стержня, Lo — длина стержня
до деформации. Коэффициент Е,
характеризующий упругие свойства материала
стержня, называется модулем Юнга.

|
Применительно к пружине закон Гука
записывается в виде:

|
где
и х = 5L — абсолютное удлинение
пружины. Силами упругости являются и так
называемые силы натяжения нити Т и реакции
опоры N .
5. Закон сохранения импульса
Импульсомматериальной точки называется
векторная величина, равная произведению ее
массы m на вектор скорости частицы v :
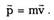
Из первого закона Ньютона следует, что
импульс свободной частицы не изменяется ни по
величине, ни по направлению, т.е. р = const. Если
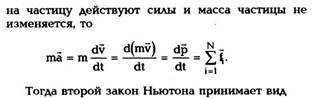
|

|
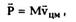
|

|

|

|

|
| Переписав (2.11) в виде |
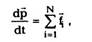
|
(2.8)

|
т.е. скорость изменения импульса частицы dp/dt
равна векторной сумме сил, действующих на нее.
Из (2.8) следует, что изменение импульса частицы
за время dt
систему взаимодействуют только между собой и
не взаимодействуют с телами, не входящими в
систему, то такая система называется замкнутой.
В противном случае система не является
замкнутой.
Импульсом системыР называется векторная
сумма импульсов всех частиц, входящих в
систему:
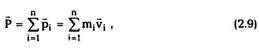
где т, — масса i-ой частицы и Vj - ее скорость в
выбранной ИСО. С течением времени импульсы
частиц изменяются, а сами частицы движутся по
каким-то своим траекториям Fj = Г|(1).

|
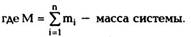
|
Центром масс(центром инерции) системы
частиц называется точка в пространстве, радиус-
вектор которой определяется из выражения:
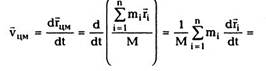
|
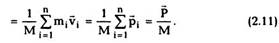
|
Найдем теперь скорость, с которой движется
центр масс системы. По определению вектора
скорости
внешних сил, действующих на систему.
Соотношение (2.14) называется вторым законом
Ньютона для системы материальных точек:
скорость изменения импульса системы равна
векторной сумме внешних сил, действующих на
систему.
Используя (2.12), уравнение (2.14) можно,
переписать в виде
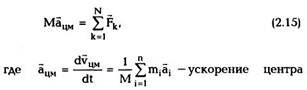
масс системы и а4 - ускорение i-ой частицы. Из
(2.15) видно, что второй закон Ньютона для
системы частиц по форме совпадает со вторым
законом Ньютона для материальной точки, только
вместо массы частицы стоит масса системы,
вместо ускорения частицы — ускорение центра
масс, а в правой части — не все, а только
внешние по отношению к системе силы.
Уравнение (2.14) можно записать в виде

где dP — бесконечно малое изменение импульса
системы за время dt под действием импульсов
внешних сил Fkdt, то есть импульс системы могут
изменить только импульсы внешних сил.
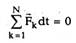
|
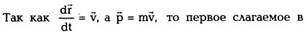
|

|

|

|
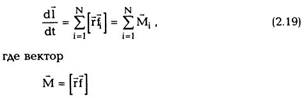
|
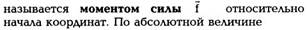
|

|
|
| Если система замкнутая, то |
| и dP = 0 , то есть импульс замкнутой системы: |
Это утверждение носит название закона
сохранения импульса.Этот закон является одним
из фундаментальных законов природы и вытекает,
вообще говоря, из свойств нашего пространства, а
именно, из свойства однородности пространства:
физические процессы, протекающие в замкнутой
системе, не зависят от положения системы в
пространстве.

|
Из соотношения (2.15) следует, что центр масс
замкнутой системы движется равномерно и
6. Закон сохранения момента
импульса
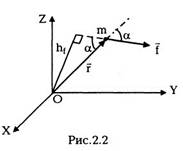
Помимо импульса р = mv , материальная точка
характеризуется еще одной динамической
переменной, которая называется моментом
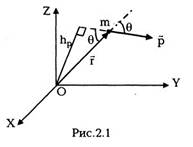
импульса. Моментом импульсачастицы I
относительно начала координат называется
векторная величина

где квадратные скобки обозначают векторное
произведение. По модулю

|

|
|

|

|

|

|
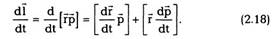
|

|
Из (2.21) видно, что для замкнутой системы
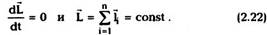
Это утверждение называется законом
сохранения момента импульса.Как и закон
сохранения импульса, этот закон вытекает из
свойства нашего пространства, которое
называется изотропностью пространства:
явления, протекающие в замкнутой системе, не
изменяются при повороте всей системы в
пространстве.
Дата добавления: 2014-10-31; просмотров: 375; Мы поможем в написании вашей работы!; Нарушение авторских прав |