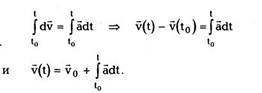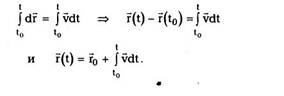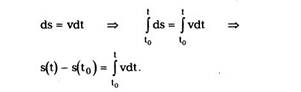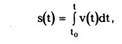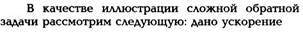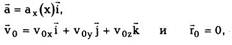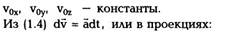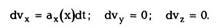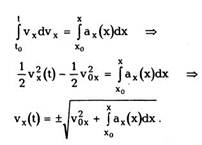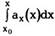КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Обратная задача кинематики
Задача кинематики бывает прямой и обратной.
В прямой задаче задается закон движения г (t), из
которого требуется получить все кинематические
характеристики движения материальной точки:

Обратная задача гораздо сложнее прямой. Это
связано не только с тем, что при ее решении
необходимо овладеть навыками интегрирования
(интегрировать всегда сложней, чем вычислять
производную), но, в основном, с тем, что заданное
ускорение а зависит, как правило, не только от
времени t, но и от координат и скорости
движущейся частицы. В результате решение
подобной задачи сводится, как правило, к
решению дифференциальных уравнений. В
простейшем случае, когда заданное ускорение а
зависит лишь от времени, решение обратной
задачи выглядит следующим образом. Из (1.4)
dv = adt, следовательно,
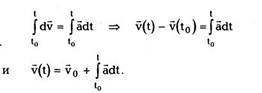
| Далее из (1.2а) следует, что dr = vdt, поэтому
|
Результат интегрирования правой части
зависит от конкретного вида зависимости а от t.
В частности, при равноускоренном движении,
когда а = const
Путь, пройденный за время t, находится с
помощью формулы (1.3), записанной в виде
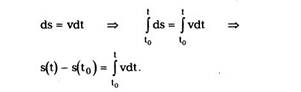
Так как s(t0) = 0, следовательно,
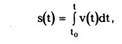
где под интегралом (не следует забывать!)
а затем интегрируют
Интеграл
в принципе вычисляется.
|