Потенциальные силы

Среди всех сил в природе существует целый
класс сил (не изменяющихся со временем),
обладающих следующим замечательным

свойством: если частица движется по замкнутому
пути, так что в результате движения она
возвращается в исходную точку, то работа,
совершаемая при этом силой, будет равна нулю.
Силы, обладающие таким свойством, называются
консервативными,или потенциальными.Если

сила f консервативна, то математически условие
потенциальности можно записать в следующем
виде:

где кружок означает, что интеграл вычисляется по
замкнутому пути L.

Кстати, интеграл типа (4.11) для произвольного

вектораА по замкнутому контуру L. Таким

образом, сила f потенциальна, если ее
циркуляция по любому замкнутому контуру равна
нулю.

Условие потенциальности можно

сформулировать другим способом: работа
консервативной силы при переносе частицы из
какой-то начальной точки 1 в конечную 2 не
зависит от вида пути, по которому происходит
перенос, а определяется только положением
начальной и конечной точек.

Действительно, рассмотрим две точки 1 и 2 и
соединим их двумя кривыми а и b (рис.4.2).
Предположим, что частица переводится из точки 1

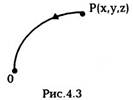
обозначим через О, за начало отсчета и будем
рассматривать работу консервативной силы при
переходе частицы из какой-либо произвольной
точки P(x,y,z) в точку О (рис.4.3). Величина этой
работы называется потенциальной энергией
частицы.находящейся в точке Р, в потенциальном
силовом поле.

Она является функцией координат х, у, z
точки Р в неподвижной системе отсчета, т.е.

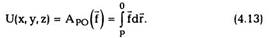
Работа консервативной силы ? (рис.4.3) при
переходе частицы из точки 1 в точку 2 (работа не
зависит от пути!):

т.е. работа консервативной силы равна убыли
потенциальной энергии.

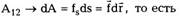
Это значит, что проекция силы на некоторое
направление s равна производной от U по
направлению s. Выражение (4.15) можно записать
в виде

откуда следует ( поскольку dU является полным
дифференциалом), что

лежит ниже нулевого уровня, z<0 и
потенциальная энергия отрицательна.

Пусть теперь имеются две частицы Мит,
которые притягиваются друг к другу силой

частицы m в точке Р, расположенной на
расстоянии г от М. Нулевой уровень выбираем на
бесконечном расстоянии от частицы М. Тогда

Такие фундаментальные силы в природе, как
гравитационная и электрическая, являются силами
консервативными, для которых можно ввести
соответствующие потенциальные энергии. Так,
например, если частица m находится вблизи
поверхности Земли, то на нее действует
гравитационная сила тяжести mg, являющаяся
консервативной.

Выбираем точку О (начало отсчета
потенциальной энергии) на какой-то высоте над
поверхностью Земли и находим потенциальную

Такое же выражение мы получим, если
зафиксируем частицу m и будем перемещать на
бесконечность частицу М, поэтому потенциальная
энергия (4.21) называется потенциальной
энергией гравитационного взаимодействиядвух
частиц m и М. Она обращается в нуль, когда
частицы удалены друг от друга на бесконечно
большое расстояние. Эта же формула остается
справедливой, если частица m находится вне
однородного шара массой М (например, планеты).
В этом случае г — расстояние от частицы m до
центра шара.

Сила упругости пружины f = kx тоже
является консервативной. Нетрудно показать, что
потенциальная энергия деформированной
пружины

энергию частицы в произвольной точке P(z)
(рис.4.5) как работу постоянной силы mg ,
направленной вертикально вниз, при

перемещении частицы из точки Р в точку О по
любому пути. Выбираем путь РАО. Тогда

так как А_РА = mgz и А_АО = 0 (здесь сила
перпендикулярна перемещению). Если точка Р

Причем нулевому уровню, как видно из (4.22),
соответствует состояние, когда пружина
недеформирована, т.е. когда х = 0.