
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
TERMINATE 5 страница
2.3.3.1 Общая постановка транспортной задачи.
В общем виде формулировка транспортной задачи осуществляется следующим образом: требуется перевезти определенное количество однородного груза из  пунктов отправления в
пунктов отправления в  пунктов назначения. Известны расходы на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения.
пунктов назначения. Известны расходы на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения.
Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь груз от поставщиков вывозится, каждый потребитель получает требуемое количество груза, и вместе с тем, общая величина транспортных издержек минимальна.
Для составления экономико-математической модели задачи введем обозначения:
 число пунктов отправления;
число пунктов отправления;
 число пунктов назначения;
число пунктов назначения;
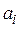 общее количество груза в i-м пункте отправления;
общее количество груза в i-м пункте отправления;
 общее количество груза, необходимое в j-м пункте назначения;
общее количество груза, необходимое в j-м пункте назначения;
 затраты на транспортировку единицы груза из i-го пункта
затраты на транспортировку единицы груза из i-го пункта
отправления в j-й пункт назначения;
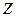 совокупные затраты на перевозку всего груза;
совокупные затраты на перевозку всего груза;
 исходно неизвестное количество груза, которое перевозится из
исходно неизвестное количество груза, которое перевозится из
i-го пункта отправления в j-й пункт назначения.
Экономико-математическая модель задачи представлена формулами (2.100)÷(2.103):
 (2.100)
(2.100)

 (2.101)
(2.101)
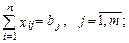 (2.102)
(2.102)
 (2.103)
(2.103)
Целевая функция (2.100) минимизирует совокупные затраты на транспортировку всех партий грузов из всех пунктов отправления во все пункты назначения. Система ограничений (2.101) говорит о том, что весь груз из каждого пункта его сосредоточения должен быть вывезен. Система ограничений (2.102) говорит о том, что потребность в грузе в каждом пункте назначения должна быть удовлетворена. Система ограничений (2.103) говорит о том, что по любому маршруту некоторое количество груза либо перевозится, либо нет.
Транспортная задача является задачей линейного программирования с (n + m) ограничениями уравнениями и (n x m) неизвестными.
Транспортная задача, у которой суммарное наличие груза совпадает с суммарной потребностью, т.е. выполняется равенство (2.104)
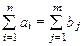 (2.104)
(2.104)
называется закрытой (сбалансированной) транспортной задачей. Если условие (2.104) выполняется, то доказано, что транспортная задача имеет оптимальное допустимое решение. В случае если условие (2.104) не выполняется, то транспортная задача называется открытой. Решение транспортных задач с открытой моделью сводится к решению задач с закрытой моделью путем добавления фиктивного поставщика или фиктивного потребителя так, чтобы выполнялось условие (2.104). Транспортная задача относится к задачам распределительного типа и решается симплексным методом. Приведем прием решения транспортной задачи с помощью средства «Поиск решения» EXCEL.
Пример 2.4. Условия транспортной задачи представлены в таблице 2.6.
Таблица 2.6
| Поставщики | Мощности поставщиков (ai) | Мощности потребителей (bj) | |||
В примере однородный груз должен быть доставлен от четырех поставщиков (n=4) четырем потребителям (m=4). Мощности поставщиков (  ) и потребность в этом грузе в каждом пункте назначения (
) и потребность в этом грузе в каждом пункте назначения (  ) приведены в таблице 2.6. В левых нижних углах каждой клетки рабочей таблицы, которые соответствуют всем возможным путям перевозки груза из всех пунктов отправления во все пункты назначения, указаны затраты на транспортировку единицы груза по данному маршруту (
) приведены в таблице 2.6. В левых нижних углах каждой клетки рабочей таблицы, которые соответствуют всем возможным путям перевозки груза из всех пунктов отправления во все пункты назначения, указаны затраты на транспортировку единицы груза по данному маршруту ( 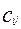 ). Суммарные запасы груза (550) и потребности в грузе (550) совпадают, значит это закрытая транспортная задача. Требуется составить план перевозок, обеспечивающий минимальные затраты на транспортировку всего груза.
). Суммарные запасы груза (550) и потребности в грузе (550) совпадают, значит это закрытая транспортная задача. Требуется составить план перевозок, обеспечивающий минимальные затраты на транспортировку всего груза.
2.3.3.2 Подготовка к решению транспортной задачи в EXCEL.
Для решения задачи средством EXCEL «Поиск решения» необходимо разместить в рабочем листе исходные данные и подготовить поля для размещения условий и результатов решения задачи (выбор ячеек листа произвольный). Таким образом будет создана «Электронная модель транспортной задачи».
На рис. 2.2 приведен пример подготовки данных на рабочем листе EXCEL для решения этой задачи.
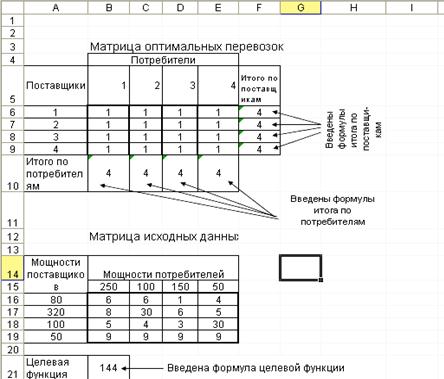
Рис. 2.2 Пример подготовки размещения данных транспортной задачи для решения в EXCEL.
Рекомендуется следующий порядок работы в рабочем листе.
1) Выделить диапазон ячеек:
− для размещения исходной матрицы (A14:E19);
− для размещения матрицы оптимальных перевозок (матрица для размещения результатов после решения задачи) (A4:F9), рекомендуется для наглядности в обе матрицы внести текст пояснений;
2) матрицу исходных данных (A14:E19) заполнить исходными данными таблицы 2.6 (значения ai, bj, cij).
В матрице результата во все ячейки диапазона (B6:E9) внести «1» в качестве исходных значений объемов поставок xij, после решения задачи в этих ячейках будут находиться значения поставок, обеспечивающие минимальные затраты на перевозку груза.
3) ввести в ячейки (В10:Е10) итог поставок по потребителям: в ячейку В10 ввести формулу =СУММ(В6:В9) − итог поставок по 1-му потребителю, скопировать эту формулу в ячейки (С10:Е10);
4) ввести в ячейки (F6:F9) итоги реализации мощности каждого из поставщиков: в ячейку F6 ввести формулу =СУММ(В6:Е6) − итог реализации поставок от 1-го поставщика, скопировать эту формулу в ячейки (F7:F9);
5) выделить ячейку для ввода формулы целевой функции, например В21и ввести формулу =СУММПРОИЗВ(В16:Е19;В6:Е9) −суммарнаястоимость перевозок по всем направлениям.
6) в рабочем окне режима «Поиск решения» указать в качестве ячейки целевой функции В21, при вводе ограниченийделать ссылку на отведенные диапазоны (см. данные таблицы 2.7):
Таблица 2.7
| Левая часть ограничения | Знак | Правая часть ограничения | Экономический смысл |
| (В10:Е10) | = | (В15:Е15) | Спрос потребителей должен быть удовлетворен |
| (F6:F9) | = | (А16:А19) | Весь груз от поставщиков должен быть вывезен |
После проведенной подготовительной работы можно запустить задачу на выполнение. В результате решения ячейки (В6:Е9)будут заполнены значениями объемов перевозок, которые обеспечивают минимальные суммарные затраты на транспортировку всего груза, а величина затрат выдается в ячейке В21.
Приведенный алгоритм подготовки электронной модели транспортной задачи может быть использован для реализации любых моделей распределительных задач, например задач оптимизации загрузки взаимозаменяемого оборудования.
Вопросы по теме
1. Сформулируйте постановку транспортной задачи.
2. Опишите математическую модель задачи прикрепления потребителей к поставщикам.
3. Как решается транспортная задача с нарушенным балансом между спросом и потреблением.
4. Приведите запись формализованной модели транспортной задачи.
5. Приведите пример постановки транспортной задачи в табличной форме при трех поставщиках и пяти потребителях.
2.4 Модели формирования оптимального портфеля ценных бумаг.
Одной из систем в рыночной экономике является инвестирование через рынок капитала, т.е. система торговли финансовыми активами и инструментами .
Рынок капитала подразделяется на рынок ценных бумаг и рынок ссудного капитала. Выпуская ценные бумаги и продавая их, получая доход от операций с ценными бумагами, предприятия получают необходимые финансовые ресурсы. Поэтому перед банками, инвестиционными фондами, отделами ценных бумаг фирм стоит вопрос формирования оптимального портфеля ценных бумаг.
2.4.1 Общие вопросы формирования портфеля ценных бумаг.
Основы теории инвестиционного портфеля впервые были разработаны нобелевским лауреатом Гарри Марковицем в статье «Выбор портфеля» в 1952г.
Портфель ценных бумаг – это совокупность ценных бумаг, приобретенных инвестором (вкладчиком). Структура портфеля – это соотношение долей капитала, вложенных в ценные бумаги определенного вида. В портфель могут входить ценные бумаги только одного типа (акции или облигации), но чаще всего различные инвестиционные ценности: акции, облигации, депозитные сертификаты, недвижимость, земля. Главная цель формирования портфеля ценных бумаг – в достижении оптимального сочетания между риском и доходом, т.е. соответствующий набор инвестиционных инстументов должен снизить до минимума риск потерь и одновременно максимизировать доход.
доход.
На рис. 2.3 представлен график с осями «Доходность» и «Риск», где отмечены точки (*), соответствующие всем возможным портфелям. Эффективным портфелям соответствуют точки, расположенные на части АВ кривой, ограничивающей эту область, Эта часть кривой называется эффективной границей. Оптимальный портфель сочетает рисковые активы с безрисковыми ценными бумагами. Наилучшее соотношение между приростом доходности и возрастанием риска обеспечивается в точке О – точке касания прямой, проведенной из точки М (доходность безрискового актива) к эффективной границе.

Рисунок 2.3 Понятие эффективного портфеля.
Портфель ценных бумаг (ПЦБ)– это сложный финансовый объект, имеющий собственную теоретическую базу. Перед каждым, кто занимается данной практикой, встают серьезные расчетные и исследовательские задачи. В ряде случаев можно говорить не о портфеле, а о некоторых элементах “теории портфеля”, в рамках которой с помощью статистических методов осуществляются наиболее выгодное распределение риска ПЦБ и оценка прибыли. Эта теория состоит из четырех основных элементов:
- оценка активов;
- инвестиционные решения;
- оптимизация портфеля;
- оценка результатов.
Мы в дальнейшем будем рассматривать "идеальный конкурентный рынок". Все участники такого рынка имеют свободный доступ ко всей информации о ценных бумагах и стремятся сформировать оптимальный портфель ценных бумаг. Спрос на этом рынке равен предложению.
Как уже было отмечено выше, качество ПЦБ оценивается сочетанием двух факторов: доходности и риска.Риск и доходностьпортфеля – две взаимосвязанные категории.
Доход, обеспечиваемый каким либо активом, состоит из двух компонентов: полученных дивидендов и дохода от изменения стоимости актива. Доход, исчисленный в % к первоначальной стоимости актива, называется доходностью этого актива.
Существуют разные определения понятия риск. Чаще всего под риском понимают вероятность убытков или недополучение доходов по сравнению с прогнозируемым вариантом. В приложении к финансовым активам рисковость актива характеризуется степенью вариации дохода (доходности), который может быть получен благодаря владению данным активом. Так, государственные ценные бумаги обладают сравнительно небольшим риском, поскольку вариация доходности по ним в стабильной, не подверженной кризисам экономике практически равна нулю. Напротив, обыкновенная акция любой компании представляет собой значительно более рисковый актив, поскольку доход по такого рода акциям может существенно варьировать. Все используемые при составлении инвестиционного портфеля оценки носят вероятностный характер. При этом доходность и риск изменяются в одном направлении, т.е. пропорциональны друг другу.
Успех инвестиций зависит от правильности распределения средств по активам. Проведенные западными экспертами эксперименты показали, что прибыль на 94% определяется выбором типа используемых инвестиционных инструментов, на 4% - выбором конкретных ценных бумаг заданного типа и на 2% - оценкой момента закупки ценной бумаги.
Общая доходность и риск инвестиционного портфеля могут меняться путем варьирования его структуры (диверсификации портфеля).
Уменьшение риска за счет диверсификации достигается за счет того, что возможные невысокие доходы по одной ценной бумаге будут компенсироваться высокими доходами по другим. Минимизация риска достигается за счет включения в портфель бумаг разных отраслей, не связанных тесно между собой, чтобы избежать синхронности циклических колебаний их деловой активности. Исследования показали, что большая часть риска портфеля устраняется, если в него входит от 8 до 20 различных ценных бумаг, дальнейшее увеличение их количества уже незначительно уменьшает риск. Свести к нулю риск невозможно, т.к. риск портфеля состоит из двух частей: уникального риска и рыночного риска (см. Рис. 2.4).
Диверсификацией можно снизить только уникальный (специфический) риск, т.е. конкретный риск для каждого предприятия, не зависящий от общего состояния экономики. Рыночный риск (систематический) не поддается диверсификации.

Рисунок 2.4 Составляющие риска портфеля ценных бумаг.
Этот риск обусловлен внешними событиями, влияющими на рынок в целом: инфляция, экономический спад, высокие ставки %, война и др. На систематический риск приходится от 25 до 50% общего риска и, поскольку в такой ситуации затрагиваются все компании, очевидно, что систематический риск нельзя устранить диверсификацией.
В процессе управления инвестиционным портфелем необходимо постоянно решать задачу отбора финансовых активов и анализа возможности их включения в портфель. Наибольшую известность для оценки доходности финансовых активов получили модель CAPM (Capital Asset Pricing Model) и модель арбитражного ценообразования АРТ (Arbitrage Pricing Theory).
Модель САРМ (предпосылки сформулированы М.Дженсеном в 1972 г.) может быть представлена следующей формулой:
 , (2.105)
, (2.105)
где Кl – ожидаемая доходность акций данной компании;
Krf - доходность безрисковых ценных бумаг (государственные ценные бумаги);
Km - ожидаемая доходность в среднем на рынке ценных бумаг;
b - бета-коэффициент данной компании.
Показатель (Km – Krf) представляет собой рыночную (т.е. в среднем) премию за риск вложения своего капитала не в безрисковые государственные ценные бумаги, а в рисковые ценные бумаги (акции, облигации предприятий, корпораций и пр.).
Показатель (Kl – Krf) представляет собой премию за риск вложения капитала в ценные бумаги именно данной компании.
Модель САРМ означает, что премия за риск вложения капитала в ценные бумаги именно данной компании прямо пропорциональна рыночной премии за риск.
Модель САРМ позволяет спрогнозировать доходность финансового актива. В свою очередь, зная этот показатель и имея данные об ожидаемых доходах по этому активу, можно рассчитать его теоретическую стоимость.
Систематический риск в модели САРМ измеряется с помощью b - коэффициентов (бета – коэффициентов). Каждый вид ценной бумаги имеет собственный b - коэффициент, представляющий собой индекс доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг. Значение показателя b рассчитывается по статистическим данным для каждой компании, котирующей свои ценные бумаги на бирже, и периодически публикуются в специальных справочниках. Для каждой компании b - коэффициент меняется с течением времени и зависит от многих факторов, имеющих отношение к характеристике деятельности с позиции долгосрочной перспективы.
В целом по рынку ценных бумаг b - коэффициент равен единице; для отдельных компаний он колеблется около единицы, причем большинство b - коэффициентов находится в интервале от 0,5 до 2,0.
Интерпретация b - коэффициента для акций конкретной компании заключается в следующем:
b=1 означает, что акции данной компании имеют среднюю степень риска, сложившуюся на рынке в целом;
b<1 означает, что ценные бумаги данной компании менее рискованны, чем в среднем на рынке;
b>1 означает, что ценные бумаги данной компании более рискованны, чем в среднем на рынке;
увеличение b - коэффициента в динамике означает, что вложения
в ценные бумаги данной компании становятся более рискованными;
снижение b - коэффициента в динамике означает, что вложения
в ценные бумаги данной компании становятся менее рискованными.
С 1995 г. b - коэффициенты появились и на отечественном рынке ценных бумаг. Так, в 1997г. нефтедобывающая отрасль имела b=0,93, а нефтехимическая - b=0,18. Значения b - коэффициентов периодически публикуются в газете "Финансовые известия".
Недостаток модели САРМ состоит в том, что:
1) она сопровождается целым рядом теоретических предпосылок, часть из которых не могут быть выполнены на практике, например: принимается, что деятельность инвесторов по покупке и продаже ценных бумаг не оказывает влияния на уровень цен на рынке этих бумаг, что все инвесторы находятся в одинаковых условиях, что отсутствуют расходы на покупку и продажу ценных бумаг; не принимаются во внимание налоги.
2) это однофакторная модель зависимости доходности от рыночного риска.
Известны и другие подходы, альтернативные модели САРМ, например, модель АРТ (модель теории арбитражного ценообразования).
Модель АРТ(автор Стивен Росс)лишена этих недостатков и может быть представлена формулой (2.106):
 (2.106)
(2.106)
где:
K^j – фактическая доходность j-ой ценной бумаги;
Kj – ожидаемая доходность j-ой ценной бумаги;
f^i-– фактическое значение i-го экономического фактора;
fi-– ожидаемое значение i-го экономического фактора;
bjn – чувствительность j-ой ценной бумаги к i-ому экономическому фактору;
ej – влияние не включенных в модель специфических факторов на изменение доходности j-ой ценной бумаги.
В основу модели АРТ заложено утверждение о том, что фактическая доходность любой акции складывается из двух частей: нормальной (ожидаемой) доходности и рисковой (неопределенной) доходности. Последняя составляющая определяется многими экономическими факторами, например, рыночной ситуацией в стране, оцениваемым ВВП, стабильностью мировой экономики, инфляцией, динамикой процентных ставок и др. Достоинство модели состоит в том, что доходность актива является функцией многих переменных, нет таких жестких предпосылок, как в модели САРМ, количество и состав внешних факторов определяется аналитиком и заранее не регламентируется.
Фактическая реализация модели требует привлечения сложного аппарата математической статистики.
2.4.2 Экономико-математические модели оптимизации портфеля ценных бумаг
При формировании портфеля возможны три основные формулировки задач оптимизации:
1) целевая функция – максимизация доходности, остальное – в ограничения;
2) целевая функция – минимизация риска, остальное – в ограничения;
3) двухмерная оптимизация по параметрам “доходность-надежность” c последующим получением некоторого приемлемого значения комбинации "доходность – риск".
Одним из ограничений в этих моделях может быть ликвидность портфеля ценных бумаг на случай непредусмотренной ранее необходимости срочного расформирования всего портфеля. Уровень ликвидности определяется как число дней, необходимых для полной конвертации всех активов портфеля в денежные средства и перевода их на счет клиента.
Для получения количественных характеристик портфеля используются следующие зависимости:
Доходность портфеля рассчитывается как средневзвешенная доходность его составляющих:
 , (2.107)
, (2.107)
где:
xi доля инвестиций, помещенных в i-ый актив (портфельный вес i-го актива),
di – ожидаемая ставка дохода по i-му активу,
n – число активов в портфеле.
Риск портфеля dp определяется как стандартное отклонение доходности по портфелю (dp 2 - дисперсия доходности)
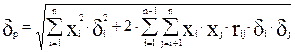 (2.108)
(2.108)
где
di ─ стандартное отклонение доходности по i-активу,
rij ─ коэффициент корреляции доходностей i-го и j-го активов.
Варьируя портфельные веса xi применяемых в составе портфеля активов, можно добиться оптимального, с точки зрения применяемого типа, портфеля.
Модель портфеля максимальной доходностипредставлена формулами (2.104)÷(2.111):
целевая функция:
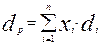 max (2.104)
max (2.104)
при ограничениях:
риск портфеля не должен превышать заданной величины
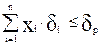 (2.110)
(2.110)
все средства должны быть полностью инвестированы:
 (2.111)
(2.111)
Модель портфеля минимального риска представлена формулами (2.112)÷(2.114):
целевая функция:

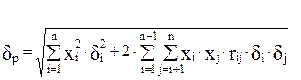 min (2.112)
min (2.112)
при ограничениях:
доходность портфеля должна быть не меньше заданной величины
 (2.113)
(2.113)
все средства должны быть полностью инвестированы:
 (2.114)
(2.114)
В результате решения этих задач находятся доли капитала xi ,  эффективного портфеля.
эффективного портфеля.
Если xi > 0, то это означает, что инвестор должен вложить xi долю своего капитала в i-вид ценных бумаг.
Если же xi < 0, то инвестору следует взять в долг ценные бумаги i-го вида на сумму, равную xi долей своего капитала. Если взятие в долг невозможно, то в задачу следует ввести дополнительное ограничение:
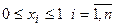 (2.115).
(2.115).
Для решения задач с дополнительным условием неотрицательности переменных и без него разработаны пакеты прикладных программ, но можно использовать и возможности электронной таблицы EXCEL.
Вопросы по теме
1. Дайте определение портфеля ценных бумаг (ПЦБ).
2. Понятие структуры ПЦБ.
3. Как оценивается качество ПЦБ.
4. Понятие диверсификации ПЦБ.
5. Способы оценки доходности финансовых активов.
6. Возможные модели оптимизации ПЦБ и составляющие моделей.
Раздел III Модели исследования операций.
Существует большое количество экономических задач, в которых невозможно однозначно определить основные параметры и переменные модели изучаемого процесса или явления. В этом случае говорят, что принятие хозяйственных решений осуществляется в условиях неопределенности. Тогда предполагается для неопределенных параметров получить вероятностные характеристики (функцию плотности вероятности, среднее значение, дисперсию). В конечном счете делают вывод о допустимом варианте хозяйственного решения по некоторому, как правило, заранее определенному пороговому критерию
3.1 Модели систем массового обслуживания (СМО)
Во многих областях экономики, финансов, производства и быта важную роль играют системы, реализующие многократное выполнение однотипных задач. Такие системы называются системами массового обслуживания (СМО). Примерами СМО являются: банки различных типов, страховые организации, налоговые инспекции, аудиторские службы, различные системы связи, погрузочно-разгрузочные комплексы, автозаправочные станции, различные предприятия и организации сферы обслуживания.
3.1.1 Общие сведения о системах массового обслуживания
Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а в случайные моменты времени. Обслуживание заявок также длится не постоянное, заранее известное время, а случайное, которое зависит от многих случайных, порой неизвестных нам, причин. После обслуживания заявки канал освобождается и готов к приёму следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО. В некоторые промежутки времени на входе СМО могут скапливаться заявки, что приводит к перегрузке СМО, в некоторые же другие интервалы времени при свободных каналах (устройствах обслуживания) на входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к простаиванию её каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по какой-то причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными.
На рис 3.1 изображена схема СМО.
Основными элементами (признаками) систем массового обслуживания являются:
Обслуживающий узел (блок),
Поток заявок,
Очередь в ожидании обслуживания (дисциплина очереди).
Обслуживающий блок предназначен для осуществления действий согласно требованиям поступающих в систему заявок.


Рис. 3.1 Схема системы массового обслуживания
Вторая составляющая систем массового обслуживания — входной поток заявок. Заявки поступают в систему случайным образом. Обычно предполагают, что входной поток подчиняется некоторому вероятностному закону для длительности интервалов между двумя последовательно поступающими заявками, причем закон распределения считается не изменяющимся в течение некоторого достаточно продолжительного времени. Источник заявок — неограничен.
Третья составляющая — дисциплина очереди. Эта характеристика описывает порядок обслуживания заявок, поступающих на вход системы. Поскольку обслуживающий блок, как правило, имеет ограниченную пропускную способность, а заявки поступают нерегулярно, то периодически создается очередь заявок в ожидании обслуживания, а иногда обслуживающая система простаивает в ожидании заявок.
Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны: обслуживаемая и обслуживающая. Случайное поведение хотя бы одной из сторон приводит к случайному характеру протекания процесса обслуживания в целом. Источниками случайности взаимодействия этих двух сторон являются случайные события двух типов.
Дата добавления: 2014-11-13; просмотров: 321; Мы поможем в написании вашей работы!; Нарушение авторских прав |