
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. 1. Назначение задач развития и размещения производств.
1. Назначение задач развития и размещения производств.
2. Классификация задач развития и размещения производств (РРП).
3. Различия в модели простой транспортной задачи от простой одноэтапной однономенклатурной модели задачи РРП.
4. Что означает целочисленность решения задачи РРП.
5. Каким образом преодолевается в моделях задач РРП нелинейность зависимости затрат от объемов производства.
6. Составьте экономико-математическая модель к задаче раздела 4.2.7.
Раздел V. Экономико-математические модели социально-экономических систем
В условиях рыночной экономики в основе принятия хозяйственных решений лежит рыночная информация, а обоснованность решений проверяется рынком в ходе реализации товаров и услуг. Поэтому начальным этапом предпринимательской деятельности должно быть изучение потребительского спроса. В этом разделе рассматриваются некоторые вопросы моделирования спроса и потребления.
5.1 Математические модели анализа потребительского поведения и спроса
5.1.1 Анализ полезности товаров, кривые безразличия.
В качестве основных факторов потребительского выбора рассматриваются полезность товара, цена на товар, доход покупателя. Существуют два основных подхода к анализу полезности как основного фактора потребительского выбора – количественный и порядковый.
Количественный подход к анализу полезности основан на представлении о возможности измерения полезности различных благ в гипотетических единицах - ютилах (utility-полезность). Количественная функция общей полезности (TU) вначале возрастающая, имеет точку максимума (S), после которой она становится убывающей (см. рис.5.1).
Предельная полезность (MU) показывает прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу и рассчитывается по следующей формуле:
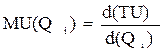 (5.1)
(5.1)
Чаще всего, как видно на рисунке 5.1, предельная полезность падает и в точке максимума становится равной нулю, а далее - отрицательной.
 TU
TU



 S
S
 |
 QA
QA
 MU
MU
 |
 QA
QA
Рис. 5.1 График функции общей (TU) и предельной (MU) полезности.
Порядковый подход к анализу полезности является более распространенным и исходит из того, что человеку присущи отношения предпочтения при оценке им полезности тех или иных товаров.
Рассмотрим основную предпосылку теории оптимального выбора потребителя: потребитель осуществляет право сравнения и свободного выбора на некотором множестве X потребительских наборов, в каждый из которых включаются все виды продукции, которые являются предметами потребления для данной группы семей (потребителей). Можно считать, что всякий такой набор состоит из фиксированного числа ( n ) элементов и имеет вид:
Х = (x1, . . . , xj, . . . , xn) ,
где элементы xj ³ 0 , поскольку они выражают количество потребляемой продукции.
Далее предполагается, что сравнительная оценка различных наборов данным потребителем с точки зрения его вкусов, привычек, традиций и т.д., может быть выражена при помощи т.н. бинарного отношения слабого предпочтения.
Это отношение определено на множестве потребительских наборов X , выражается формулой “предпочтительнее чем ...или равноценен”, записывается при помощи знака “=”.
Формула “x=y” , где x и y суть потребительские наборы означает, что данный потребитель (группа семей) в равных условиях либо предпочтет набор x набору y, либо не видит различия между ними, т.е. считает их равноценными.
На базе отношения слабого предпочтения вводится отношение безразличия (равноценности): два набора x и y безразличны для потребителя, если одновременно выполняются условия “x=y” и “y=x”. Факт равноценности двух наборов обычно записывается при помощи выражение “y ~ x”. Понятие строгого (сильного) предпочтения определяется следующим образом: “x y” тогда и только тогда, когда “x=y”, а соотношение “y= x” не имеет места.
Рассмотрим наборы только из двух товаров C и U. (Товары C и U можно рассматривать как комбинированные товары). Отношения предпочтения, характерные для каждого индивида, отражают посредством кривой безразличия, изображенной на рисунке 5.2.
Кривая безразличия отражает множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично (равноценно), какой из этих наборов выбрать.
Наборы А и В с точки зрения данного потребления равноценны и лежат на одной и той же кривой безразличия I. Для нашего потребителя любой набор, лежащий на кривой II, предпочтительнее любого набора, лежащего на кривой I и т. д.

Рис. 5.2 Кривые безразличия
Предельная норма замещения (MRS - marginal rate of substitution) - основное рабочее понятие порядковой теории полезности.
Предельной нормой замещения блага X благом Y (MRSxy) называют количество блага Y, которое должно быть сокращено «в обмен» на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:
 при условии, что U= const (5.2)
при условии, что U= const (5.2)
Выделяют следующие типы кривых безразличия в зависимости от функций полезности: кривые безразличия линейного типа; неоклассического типа; кривые безразличия функций с полным взаимодополнением благ.
Кривые безразличия линейного типа соответствуют функции полезности с полным взаимозамещением благ (чай и кофе), которая имеет следующий вид:
 (5.3)
(5.3)
где 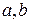 - параметры;
- параметры;
 - полезность;
- полезность;
 - товары.
- товары.
Из функции полезности (5.3) можно найти Y:
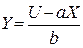 (5.4)
(5.4)
и построить кривые безразличия линейного типа (см. рис. 5.3):

Рис. 5.3 Кривые безразличия линейного типа
Неоклассическая функция полезности имеет вид:
 , где
, где  . (5.5)
. (5.5)
Чтобы построить кривые безразличия необходимо найти Y:
 (5.6)
(5.6)
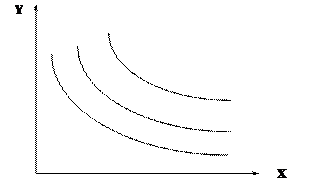
Рис.5.4 Кривые безразличия неоклассического типа
Функции с полным взаимодополнением благ имеют кривые безразличия в виде точки на пересечении двух прямых. При этом полные взаимодополнение благ предполагает, что при увеличении спроса на одно из двух благ растет спрос и на второе благо, например, сахар и чай, бензин и моторное масло. Избыток одного блага не имеет значения, полезность достигается лишь при определенной комбинации обоих благ:
 (5.7)
(5.7)

Рис. 5.5 Кривые безразличия функций с полным взаимодополнением благ
5.1.2 Решение задачи об оптимальном выборе потребителя.
Кривые безразличия графически отражают систему предпочтений потребителя. Естественно, потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Однако, это не всегда возможно, т.к. выбор набора ограничивается средствами, которыми располагает потребитель.
Обозначим рыночные цены блага X через Рх, цены блага Y через Py, доход потребителя через I; тогда бюджетное ограничение потребителя можно записать в виде уравнения:
 . (5.8)
. (5.8)
т.е. доход потребителя равен сумме его расходов на покупку товаров X и Y.
Преобразуем уравнение (5.8) и получим уравнение бюджетной линии (5.9), которая имеет вид прямой линии (рисунок 5.6). Чем выше доход, тем дальше от начала координат находится линия бюджетного ограничения.
 . (5.9)
. (5.9)
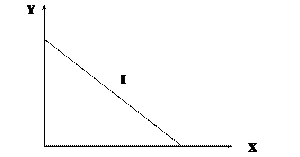
Рис. 5.6 Бюджетная линия
Пусть задана линия бюджетного ограничения и несколько кривых безразличия. В рамках бюджетного ограничения потребитель постарается так распределить свой доход между различными благами, чтобы максимизировать полезность U. Соответствующий набор благ называется оптимальным планом потребления и обычно обозначается точкой касания бюджетной линии и кривой безразличия.

Рис. 5.7 Оптимальный выбор потребителя
Для ситуации, представленной на рисунке 5.7, оптимум потребителя будет в точке С.
В точке оптимума соотношение цены блага X к цене блага Y равно предельной норме замещения блага X благом Y, т.е. выполняется равенство:
 (5.10)
(5.10)
Во многих прикладных исследованиях важную роль играет коэффициент эластичности. Под эластичностью понимают меру реагирования эндогенной (зависимой) переменной на изменение экзогенной (независимой) переменной.
Приведем также более конкретное определение: эластичность - предел соотношения между относительным приращением функции y (зависимой переменной)  и относительным приращением независимой переменной x
и относительным приращением независимой переменной x 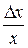 когда
когда  и обозначается Ex(y).
и обозначается Ex(y).
Таким образом, эластичность можно выразить формулой:
 при
при  (5.11)
(5.11)
или в непрерывном случае:
 . (5.12)
. (5.12)
На практике эластичность относят к проценту прироста независимой переменной. Тогда эластичность показывает, на сколько процентов повышается или понижается эндогенная переменная Y, если независимая переменная X изменяется на 1%.
Различают дуговую эластичность, то есть среднюю на каком-то отрезке кривой, и точечную эластичность - значение производной в заданной точке. Для практического вычисления эластичности используется формула английского математика и экономиста Рой Аллена (19061983). Он предложил использовать среднюю точку интервала, по которому происходит изменение, в качестве знаменателя дроби. Тогда вычисляются:
относительное изменение эндогенной переменной: 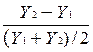
и относительное изменение экзогенной переменной:
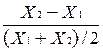 .
.
Затем вычисляется отношение первого ко второму.
Формула Аллена имеет широкое распространение, однако ее не следует применять к очень широким интервалам, поскольку в этом случае она может ввести в заблуждение.
Для определения эластичности спроса от цены можно воспользоваться формулой:
 при
при  (5.13)
(5.13)
Коэффициент эластичности спроса по цене показывает, на сколько процентов уменьшится (увеличится) спрос, если цена товара увеличится (уменьшится) на 1%.
И, наконец, существуют различные степени эластичности спроса по цене. Так, спрос неэластичен по цене, если спрос на товар практически не зависит от его цены, в этом случае коэффициент эластичности близок к нулю. Примером товаров с неэластичным спросом являются предметы первой необходимости. Спрос нормально эластичен, если Ed.p » 1, что имеет место для товаров длительного пользования. Спрос является суперэластичным для предметов роскоши Ed.p > 1.
5.2 Модели микроэкономического анализа рынка
5.2.1 Спрос, предложение, равновесная цена.
Важнейшими категориями микроэкономического анализа являются спрос и предложение на отдельных рынках.
Под спросом понимают количество товаров (услуг), которое будет куплено по определенной цене за определенный период.
Закон спроса означает, что при прочих равных условиях спрос на товары в количественном выражении изменяется в обратной зависимости от цены.
Под предложением понимают количество товаров (услуг), которое производители готовы продать по определенной цене за определенный период.
Закон предложения означает, что предложение, при прочих равных условиях, изменяется в прямой зависимости от изменения цены.
Точка равновесия – это точка пересечения кривых спроса (D - demand) и предложения (S - supply), в которой фиксируется равновесная цена.
Равновесная цена (цена равновесия) рыночная цена, которая устанавливается в результате взаимодействия спроса и предложения и устраивает одновременно и покупателя, и продавца.
 (5.14)
(5.14)
 | |||
 | |||
Рис. 5.8 Формирование равновесной цены
Выделяют следующие принципы формирования равновесной цены: во-первых, цена стремится к такому уровню, при котором спрос равен предложению; во-вторых, цена может меняться под влиянием неценовых факторов. Во втором случае к возрастанию цены приводит повышение спроса при неизменном предложении или сокращение предложения при неизменном спросе, и к снижению цены приводит сокращение спроса при неизменном предложении или увеличение предложения при неизменном спросе.
Существуют также неценовые факторы спроса и предложения.
Так, в качестве неценового фактора спроса выступают изменения в денежных доходах населения: в случае увеличения дохода (  ) кривая спроса занимает более высокое положение
) кривая спроса занимает более высокое положение 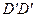 (рис.5.9) и новая цена равновесия (
(рис.5.9) и новая цена равновесия (  ) оказывается большей, чем прежняя (
) оказывается большей, чем прежняя (  ). При этом объем продаж товара в денежном выражении увеличивается (
). При этом объем продаж товара в денежном выражении увеличивается (  ).
).
 |
Рис. 5.9 Смещение кривой спроса при увеличении дохода
Неценовыми факторами спроса являются также изменение потребительских предпочтений под воздействием рекламы, моды, а также появление на рынке более дешевых и эффективных заменителей товаров. В последнем случае покупатели уменьшают ту долю дохода, которую они предназначали ранее для покупки товара (  ), и спрос на этот товар падает. В следствии этого кривая спроса сдвигается вниз и налево (рис. 5.10) и новая цена равновесия становится более низкой, нежели прежняя (
), и спрос на этот товар падает. В следствии этого кривая спроса сдвигается вниз и налево (рис. 5.10) и новая цена равновесия становится более низкой, нежели прежняя ( 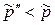 ).
).

Рис. 5.10 Смещение кривой спроса при появлении на рынке более дешевого аналогичного товара
В качестве неценовых факторов предложения выступают изменение издержек производства в результате технических нововведений, изменения стоимости факторов производства, налоговой политики. При этом при снижении издержек кривая предложения смещается налево вверх (  ) и цена равновесия уменьшается (
) и цена равновесия уменьшается (  ).
).
| 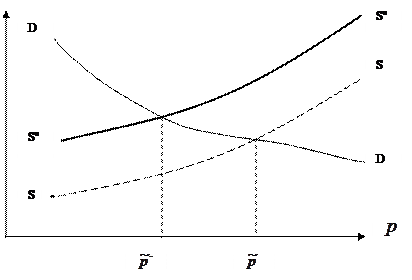 | |||
Рис. 5.11 Смещение кривой спроса при снижении издержек производства
5.2.2 Моделирование процесса достижения рыночного равновесия
Равновесная цена в конкурентной экономике без сговора достигается в результате стихийного процесса: при любой цене, превышающей равновесную, количество товара, которое стремятся предложить продавцы (производители), будет превосходить то количество, на которое покупатели (потребители) намерены предъявить спрос; в результате возникает давление на цену в сторону ее понижения. Аналогично цена, находящаяся ниже уровня равновесия, испытывает давление в сторону повышения.
По А. Маршаллу различают мгновенное, кратковременное и длительное рыночное равновесие в зависимости от цены, т.е. наличии не меняющейся во времени функции спроса D(p).
Мгновенное равновесие достигается в обстановке, когда предложение фиксировано (  ), т.е. производители товара не готовы к расширению производства или не в состоянии это сделать; равновесие такого рода обычно достигается при достаточно высокой цене
), т.е. производители товара не готовы к расширению производства или не в состоянии это сделать; равновесие такого рода обычно достигается при достаточно высокой цене  , что и является стимулом для последующих действий производителей.
, что и является стимулом для последующих действий производителей.
Кратковременное равновесие возникает тогда, когда в действие вводятся наличные резервы (свободные производственные мощности) и предложение несколько увеличивается, причем  ; равновесная цена
; равновесная цена 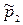 в этой ситуации оказывается ниже
в этой ситуации оказывается ниже  , но и остается еще довольно высокой.
, но и остается еще довольно высокой.
Длительное нормальное равновесие устанавливается в ситуации, когда в деле принимают участие практически все производители, способные производить данный товар без резкой перестройки своей хозяйственной деятельности. Функция предложения  также возрастающая и равновесная цена
также возрастающая и равновесная цена  соответствует нормальным издержкам производства.
соответствует нормальным издержкам производства.
Процесс приближения к нормальному равновесию во времени можно представить при помощи последовательности малых дискретных шагов; при этом функции спроса и предложения сами могут изменяться в ходе указанного процесса вследствие изменения условий производства и потребления.

Рис. 5.12 Длительное нормальное равновесие на рынке
Рассмотрим паутинообразную модель процесса достижения рыночного равновесия.
В процессе моделирования используется дискретное представление процесса с помощью так называемых “торговых” дней с номерами 
Предполагается, что к началу торгового дня t известна начальная цена товара 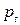 , которая полностью определяет объем предложения
, которая полностью определяет объем предложения
 . (5.15)
. (5.15)
Далее считается, что в течение дня предложенный товар полностью реализуется по цене  , которая определяется из условия временного равновесия
, которая определяется из условия временного равновесия  (5.16)
(5.16)
и является исходной ценой для следующего торгового дня (t+1) и т.д.
Геометрическая иллюстрация этого процесса приближения к равновесию (рис.5.13) напоминает паутину и поэтому сама модель часто называется паутинообразной. Можно показать, что сходимость указанного рыночного процесса будет гарантирована, если выполнено условие
 . (5.17)
. (5.17)
|
 |
|
|


Рис. 5.13 Паутинообразная модель
Последнее означает, что для сходимости достаточно, чтобы маргинальное предложение не превосходило бы маргинального спроса, или, иными словами, положительная реакция производителя на повышение цены не была бы столь же значительной как отрицательная реакция потребителя, т.е. это процесс в обстановке относительно неактивных производителей. Заметим, что если  , то возникает ситуация так называемого “свиного цикла”, при которой состояние равновесия оказывается недостижимым. В случае, если наклон линии спроса круче наклона линии предложения, спираль будет раскручиваться в обратном порядке. Если наклоны линий спроса и предложения одинаковы, то паутина закольцуется (Рис. 5.14):
, то возникает ситуация так называемого “свиного цикла”, при которой состояние равновесия оказывается недостижимым. В случае, если наклон линии спроса круче наклона линии предложения, спираль будет раскручиваться в обратном порядке. Если наклоны линий спроса и предложения одинаковы, то паутина закольцуется (Рис. 5.14):
 |
Рис. 5.14 Закольцованная паутинообразная модель
(равновесие на рынке недостижимо)
Рассмотрим ситуацию наличия активных производителей, готовых сразу же откликнуться на возникающий спрос. В этом случае процесс задается при помощи следующей системы соотношений:
- в торговый день t задано предложение  и оно определяет цену
и оно определяет цену 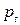 как решение уравнения (5.18):
как решение уравнения (5.18):
 . (5.18)
. (5.18)
- эта цена характеризует объем спроса:
 (5.19)
(5.19)
- а предложение на следующий торговый день прямо ориентируется на спрос предыдущего дня:
 (5.20)
(5.20)
Описанный процесс также может быть представлен при помощи паутинообразной модели, причем достаточное условие сходимости имеет вид:  что соответствует более сильной реакции производителей по сравнению с потребителями.
что соответствует более сильной реакции производителей по сравнению с потребителями.
Рассмотрим процесс достижения равновесия на следующем примере.
Пусть функция предложения S(p) = 4p - 3,
а функция спроса 
Основное соотношение имеет вид:

Отсюда цена в каждый следующий рыночный день определяется через цену в предыдущий день по формуле:

Предположим, что начальная цена  , и сведем результаты расчета в таблицу 5.1.:
, и сведем результаты расчета в таблицу 5.1.:
Сходимость цены к равновесной во времени Таблица 5.1
| p | D | S | Δ =D-S |
| 1,5 | 6,67 | 3,67 | |
| 2,42 | 4,14 | 6,67 | -2,53 |
| 1,78 | 5,61 | 4,14 | 1,47 |
| 2,15 | 4,65 | 5,61 | -0,96 |
| 1,91 | 5,23 | 4,65 | 0,58 |
| 2,06 | 4,85 | 5,23 | -0,38 |
| 1,96 | 5,10 | 4,85 | 0,25 |
| 2,02 | 4,95 | 5,10 | -0,15 |
| 1,99 | 5,02 | 4,95 | 0,07 |
| 2,01 | 4,98 | 5,02 | -0,04 |
| 2,00 | 4,98 | 0,02 |
Таким образом, мы видим, что по прошествии 11 “рыночных” дней процесс установления цены сходится к состоянию равновесия, причем получается уже известное нам значение равновесной цены  . Заметим, что промежуточные значения цены попеременно становятся то больше, то меньше равновесной величины. Это означает, что процесс имеет колебательный характер с уменьшающейся амплитудой (см. рис. 5.15).
. Заметим, что промежуточные значения цены попеременно становятся то больше, то меньше равновесной величины. Это означает, что процесс имеет колебательный характер с уменьшающейся амплитудой (см. рис. 5.15).
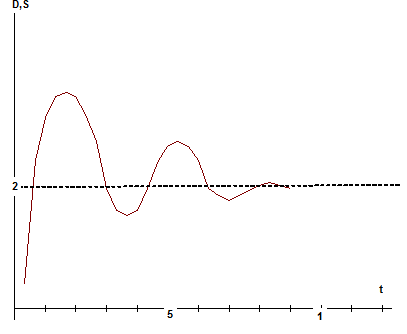
Рис.5.15 Процесс сходимости цены к равновесной.
ЛИТЕРАТУРА
1. Основная
1.1 Дорохина Е.Ю., Халиков М. А. Моделирование микроэкономики. ─М.: ЭКЗАМЕН, 2003.
1.2 Экономико-метематические методы и модели. Под ред. проф. А.В. Кузнецова. ─ Минск: БГЭУ, 2000.
1.3 Экономико-математические методы и прикладные модели / под ред. Федосеева В.В. – М.: ЮНИТИ, 1999.
1.4 Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. Учебное пособие для ВУЗов. ─ М.: ЮНИТИ-ДАНА, 2000.
1.5 Экономико-математическое моделирование. Под ред. проф. И.Н.Дрогобыцкого. Учебник. ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ РФ. – М.:ЭКЗАМЕН, 2004.
1.6 Федосеев В.В., Эриашвили Н.Д. Экономико-математические методы и модели в маркетинге. Учебное пособие для ВУЗов. / Под ред. В.В. Федосеева. ─ М.:
1.7 Шелобаев С. И. Экономико-математические методы и модели. Второе издание. ─ М.: ЮНИТИ, 2005.
2 Дополнительная
2.1 Абчук В.А. Экономико-математические методы. ─СПб: Союз, 1999.
2.2 Багриновский К.А., Матюшок В.М. Экономико-математические методы и модели (микроэкономика). – М.: Изд-во Российского университета дружбы народов, 1999.
2.3 Большаков А.С. Моделирование в менеджменте. Учебное пособие. - М.: Филинъ, 2000.
3 Горчаков А.А., Орлова И.В. Компьютерные экономико-математические модели. – М.: «Компьютер» Изд-во ЮНИТИ, 1995.
4 Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике. Под общей ред. Сидоровича А.В. 2-ое издание. – М.: Дело и сервис, 1999.
5 Ильченко А.Н. Экономико-математические методы. М.: Финансы и статистика, 2006.
6 Лопатников Л.И. Экономико-математический словарь 4-е издание – М.: Наука, 1996.
7 Монахов А. В. Математические методы анализа экономики. Учебное пособие. СПб.: ПИТЕР, 2002.
8 Малыхин В.И. Математика в экономике. Учебное пособие. ─ М.: ИНФРА-М, 2001.
9 Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в вреде Excel / Практикум. Учебное пособие для ВУЗов. - М.: Финстатинформ, 2000.
10 Тарасевич В.М. Экономико-математические методы и модели в ценообразовании. В 2-х частях – Л.: ЛФЭИ, 1991 .
11 Томас Р. Количественные методы анализа хозяйственной деятельности / пер. с англ. - М.: Дело и сервис, 1999.
12 Хайман Д.Н. Современная микроэкономика: анализ и применение. В 2-х томах. Пер. с англ. – М.: Финансы и статистика, 1992.
13 Шрайбер Т.Дж. Моделирование на GPSS. Пер. с англ. Под ред Файнберга. – М.: Машиностроение, 1980.
14 Эддоус М., Стэнннсфилд Р. Методы принятия решений / Пер. с англ. под ред. член-корр. РАН И.И.Елисеевой. – М.: Аудит, ЮНИТИ, 1997.
[1] Гранберг А.Г. Моделирование социалистической экономики. – М.: Экономика, 1988.
Введение
Предметом изучения дисциплины «Математика (Экономико-математическое модели)» являются количественные характеристики процессов, протекающих в социально-экономических системах различного уровня, изучение их взаимосвязей на основе экономико-математических методов и моделей.
Экономико-математическая модель может рассматриваться как математическое описание социально-экономической системы, которое отражает существенные свойства системы и замещает ее в процессе исследования. Построение экономико-математической модели необходимо рассматривать в качестве основного этапа более широкого процесса – экономико-математического моделирования, представляющего собой метод исследования экономической системы при помощи экономико-математических моделей.
Экономико-математическое моделирование тесно связано с компьютеризацией и является быстроразвивающимся направлением экономической науки.
Цель дисциплины – дать комплексное изложение теоретических и методологических принципов при постановке, решении и анализе задач управления экономикой на разных уровнях на основе методов математического моделирования и современных компьютерных технологий.
Основными задачами курса являются:
- овладение методологией построения и применения систем математических моделей планирования в социально-экономических системах;
- разбор типовых моделей, используемых в аналитической экономической работе на разных уровнях управления;
- освещение методов исследования результатов решения прикладных экономико-математических моделей и их использование при обосновании экономических решений.
Для решения поставленных задач определен круг вопросов, определяющих содержание отдельных разделов пособия.
В первом разделе «Теоретические основы экономико-математических моделей и моделирования» систематизированы теоретические предпосылки оптимизации социально-экономических систем, рассматриваемых в качестве объекта управления.
В рамках второго раздела «Экономико-математические модели планирования и анализа хозяйственной деятельности предприятия» – дается методология построения и анализа экономико-математических моделей: формирования производственной программы предприятия, моделей рационального использования ресурсов предприятия, моделей формирования оптимального портфеля ценных бумаг.
Третий раздел «Модели исследования операций» посвящен рассмотрению системы моделей для анализа таких экономических систем, в которых процессы протекают в условиях неопределенности и носят статистический характер. Дается понятие моделей систем массового обслуживания, приводятся основы имитационного моделирования и математического аппарата производственных функций и его использования в моделировании объемов производства, даны принципы построения моделей управления запасами на предприятиях.
В рамках четвертого раздела – «Модели народно-хозяйственного, отраслевого и регионального регулирования» – преимущественно речь идет о содержании модели межотраслевого баланса, ее использовании для народнохозяйственного регулирования структуры валового выпуска, а также для регулирования денежного оборота и составления балансов труда. Раскрывается содержание системы моделей оптимального развития и размещения крупных производств в отдельных регионах.
В пятом завершающем разделе курса «Экономико-математические модели социально-экономических систем» приводится характеристика математических моделей анализа потребительского поведения и спроса, моделей микроэкономического анализа рынка.
Изложение материала пособия опирается на знания, полученные студентами при изучении курсов «Экономическая теория», «Экономика фирмы», «Микроэкономика» и других дисциплин прикладной экономики. Инструментальной основой рассматриваемых в пособии моделей принятия оптимальных управленческих решений в сложных экономических системах являются дисциплины: «Высшая математика», «Теория вероятностей», «Математическая статистика» и «Математика (Экономико-математические методы)».
В результате изучения курса студенты должны получить теоретические знания о принципах построения экономико-математических моделей, приобрести практические навыки их представления и реализации на персональных компьютерах и экономической интерпретации полученных результатов. Эти знания должны стать платформой для освоения в дальнейшем таких дисциплин как информационные технологии в различных областях экономики.
Дата добавления: 2014-11-13; просмотров: 297; Мы поможем в написании вашей работы!; Нарушение авторских прав |