
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экономико-математические модели составления производственной программы предприятия.
Рассмотрим методологические и методические вопросы составления портфеля заказов предприятия в применении к простым по экономическому содержанию моделям и методам.
2.1.1Пример составления экономико-математической модели задачи формирования производственной программы предприятия.
Постановка задачи: цех выпускает три вида изделий, производственные возможности цеха характеризуются следующими данными:
• суточный фонд времени работы оборудования 780 часов;
• суточный расход сырья 850 тонн;
• суточный расход электроэнергии 790 квт-час.
Нормы затрат производственных ресурсов на единицу различных изделий приведены в таблице 2.1:
Таблица 2.1
| Ресурс | Ед. изм. | Изделия, расход ресурса на производство одного изделия | Суточный лимит (запас ресурса) | ||
| X1 | X2 | X3 | |||
| Оборудование | часы | ||||
| Сырье | тонны | ||||
| Электроэнергия | квт-час | ||||
| Оптовая цена | тыс.руб |
Составить план производства, обеспечивающий максимальный объем выпуска продукции в стоимостном выражении.
Запись условия задачи в виде представленной таблицы 2.1 с объяснением данных является экономической моделью задачи.
Математическая модель задачи может быть представлена в следующем виде:
Пусть х1, х2 и х3 – искомые объемы выпуска 1-го, 2-го и 3-его видов изделий.
Требуется найти неотрицательные значения переменных х1, х2 и х3, обеспечивающих максимальный по стоимости выпуск продукции.


Совокупность выражений (2.1)÷(2.7) представляет собой математическую модель задачи.
Математическая модель задачи выражений состоит из критерия оптимальности (2.1) и системы ограничений (2.2)÷(2.7). В последней можно выделить ограничение неотрицательности (2.5)÷(2.7), показывающее, какие значения могут принимать переменные., а также основные ограничения (2.2)÷(2.4), указывающие, какие преобразования можно проводить с переменными. Система ограничений определяет множество допустимых значений переменных, из которых с помощью критерия оптимальности и отыскиваются наилучшие (по данному критерию) значения.
Запишем экономико-математическую модель рассмотренной задачи в общем виде, т.е. в символах.
Введем обозначения:
 индекс ресурсов (
индекс ресурсов ( 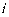 = 1, 2, ….,
= 1, 2, ….,  );
);
 индекс изделия (
индекс изделия (  = 1, 2, ….,
= 1, 2, ….,  );
);
 наличный объем
наличный объем 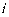 -го ресурса;
-го ресурса;
 норма затрат
норма затрат 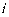 -го ресурса на производство единицы
-го ресурса на производство единицы  -го
-го
изделия;
 оптовая цена единицы изделия
оптовая цена единицы изделия  -го вида;
-го вида;
 искомый объем производства
искомый объем производства  -го изделия.
-го изделия.
В данных обозначениях задача запишется следующим образом.
Найти значения переменных  , максимизирующие целевую функцию вида
, максимизирующие целевую функцию вида

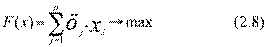
при выполнении ограничений на использование ресурсов:

и неотрицательности переменных:


Выражение (2.8) максимизирует совокупный эффект от всего объема выпущенных изделий всех видов. Выражение (2.9) означает, что для любого из ресурсов его суммарный расход на производство изделий всех видов не превосходит всего имеющегося объема (выделенного лимита). Левая часть выражения показывает используемый в оптимальном плане обьем i-го ресурса, а правая часть имеющийся обьем этого же ресурса. Выражение (2.10) означает неотрицательность выпусков изделий.
Особенность экономико-математической модели (2.8)÷(2.10) состоит в том, что она справедлива для любого количества видов продукции и ресурсов, для самых разнообразных численных значений лимитов ресурсов и норм затрат ресурсов. Коэффициенты при неизвестных в целевой функции означают эффективность от выпуска единицы продукции (прибыль, цена).
Таким образом, экономико-математическая модель (2.8)÷(2.10) соответствует любой экономической задаче по отысканию максимума эффекта от выпуска продукции при ограничениях на количество используемых ресурсов (при условии линейной зависимости эффекта и использования ресурсов от объема выпуска).
Задача формирования производственной программы может быть поставлена и на минимум целевой функции. Например, необходимо
отобрать в план такие изделия, чтобы суммарные затраты на изготовление продукции были минимальными. Если принять, что  ─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:
─ затраты на производство одной единицы j-го вида продукции, то простую модель с критерием оптимальности минимум затрат на весь объем выпуска можно представить так:
 (2.11)
(2.11)
 (2.12)
(2.12)
 (2.13)
(2.13)
Для модели такого вида существует простое оптимальное решение все неизвестные равны нулю. Действительно, при  все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
все ограничения выполняются, т.е. решение допустимо и дает наименьшее значение критерия оптимальности, т.е. затраты равны нулю. Такое правильное математическое решение приводит к абсурдному с экономической точки зрения выводу: ничего не производить и все ресурсы останутся неиспользованными.
В этой упрощенной модели не учтена цель производства получение результата в виде конечной продукции, а в процессе производства необходимо сопоставление затрат и результатов. Очевидно, необходимо ввести дополнительное ограничение, которое позволило бы не сводить к нулю затраты. В данном случае задача должна быть поставлена следующим образом: минимизация затрат при фиксированном уровне результата.
Рассмотрим экономико-математическую модель задачи на минимум затрат при фиксированных планах производства.
 (2.14)
(2.14)

 (2.15)
(2.15)
 (2.16)
(2.16)
Но любой сверхплановый выпуск увеличит значение критерия оптимальности. Ясно, что наименьший уровень затрат возможен лишь при строгом выполнении плановых заданий, т.е. при  , а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором
, а значит данная модель теряет смысл, т.к. оптимальный план известен он определяется набором 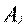 .
.
Ограничить минимум затрат снизу можно при другой постановке задачи. Пусть  цена на продукцию
цена на продукцию  -го вида, а
-го вида, а  план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:
план по валовой продукции, т.е. запланированный уровень валового дохода от выпуска продукции. Тогда модель на минимум затрат запишется так:
 (2.17)
(2.17)

 (2.18)
(2.18)
 (2.19)
(2.19)
 (2.20)
(2.20)
Постановка задачи на минимум затрат имеет смысл и в том случае, если существует несколько способов производства одноименной продукции. Например, изделия проходят обработку на токарных станках, но рабочими разной квалификации, или с использованием разных технологических способов (приспособлений). В модели
 (2.21)
(2.21)

 (2.22)
(2.22)
 (2.23)
(2.23)
 (2.24)
(2.24)
плановое задание по выпуску продукции 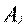 осуществляется подбором разных величин
осуществляется подбором разных величин  , для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
, для которых отбираются те рабочие или организационно-технологические приемы (обозначенные как s), которые обеспечивают минимум затрат.
Дата добавления: 2014-11-13; просмотров: 1428; Мы поможем в написании вашей работы!; Нарушение авторских прав |