Модели оптимизации загрузки невзаимозаменяемого оборудования.

В задачах загрузки невзаимозаменяемого оборудования возможно использование различных критериев оптимизации, в том числе и рассмотренных ранее. В этом случае задача оптимизации загрузки оборудования сводится к подбору оптимальной производственной программы, позволяющей наилучшим образом использовать имеющиеся производственные мощности. Отличие модели оптимальной загрузки невзаимозаменяемого оборудования от более общей задачи оптимального использования ресурсов (2.8)÷(2.10) заключается в экономическом истолковании лимитов ресурсов и норм затрат ресурсов .

Введем для моделей загрузки оборудования следующие обозначения:

­ индекс вида оборудовании,

­ норма затрат станочного времени работы -ого оборудования на производство единицы -ой продукции,

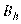­ полезный (эффективный фонд) времени оборудования вида .

Основной вид модели подбора программы под имеющиеся мощности может быть следующим:

(2.39)

(2.40)

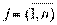(2.41)

где - прибыль от единицы j – той продукции,

- нормы затрат времени h- той группы оборудования на единицу j- той продукции,

- эффективный фонд времени работы h- той группы оборудования.

Требуется определить объем выпуска j - той продукции ( ) с целью получения максимального объема прибыли в пределах имеющихся мощностей. Здесь мы имеем частное проявление общей задачи на максимум результата при использовании ограниченного количества ресурсов.

В задаче загрузки оборудования может быть использован критерий максимума загрузки оборудования. Использование критерия на максимум загрузки может быть оправдано, ибо возможный выбор более станкоемкой продукции означает выбор более сложной в изготовлении (следовательно, и более дорогой, как правило, по цене или более прибыльной) продукции. Если нам неизвестны потребительские качества продукции, ее прибыль, себестоимость или мы можем ими пренебречь (например, значения этих показателей достаточно близки для разных видов продукции), то результатом производства может служить выпуск продукции вообще. Оптимизировать результаты производства в этом случае возможно, например, через затраты станочного времени. В этом случае целевая функция может быть представлена так:

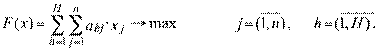(2.42)

Как правило, для одной и той же экономической задачи может быть представлено несколько моделей. В частности задача максимума загрузки оборудования может быть поставлена иначе. Вспомним, что для решения задачи методом линейного программирования система ограничений (неравенства) представляются в виде уравнений добавлением в левую часть неравенств новых переменных ­ дополнительных неизвестных , экономический смысл которых в нашей задаче ­ неиспользованный остаток фонда времени работы -ого оборудования. Так как все дополнительные неизвестные так же будут измеряться в станко-часах, то их сумма означает совокупный неиспользуемый остаток фонда времени работы оборудования всех видов. В этом случае модель на максимум загрузки оборудования можно записать следующим образом:

(2.43)

(2.44)

(2.45)

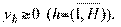(2.46)

Если заданы плановые задания по выпуску продукции вида

, (2.47)

то можно решить задачу по отысканию значений сверхпланового выпуска продукции , максимизирующих загрузку свободных остатков станочного времени. Обозначим свободные остатки фондов работы оборудования после обязательного выполнения плана

(2.48)

Модель задачи поиска сверхплановой продукции по критерию максимума загрузки оборудования примет вид

(2.53)

(2.54)

(2.55)

(2.56)

После решения задачи значения исходных переменных могут быть получены простым суммированием: .

Введение в модель ограничений по производственной программе, как и в задаче на максимум прибыли, целесообразно лишь при существовании нескольких способов производства одноименной продукции. Тогда оптимизация становится возможной за счет выбора наилучших способов производства каждой продукции в рамках заданных фиксированных планов их выпуска:

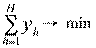(2.53)

(2.54)

(2.55)

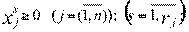(2.56)

(2.57)