Общая постановка транспортной задачи.

В общем виде формулировка транспортной задачи осуществляется следующим образом: требуется перевезти определенное количество однородного груза из пунктов отправления в пунктов назначения. Известны расходы на перевозку единицы груза из каждого пункта отправления в каждый пункт назначения.

Требуется составить такой план прикрепления потребителей к поставщикам, т.е. план перевозок, при котором весь груз от поставщиков вывозится, каждый потребитель получает требуемое количество груза, и вместе с тем, общая величина транспортных издержек минимальна.

Для составления экономико-математической модели задачи введем обозначения:

­число пунктов отправления;

­ число пунктов назначения;

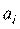­ общее количество груза в i-м пункте отправления;

­ общее количество груза, необходимое в j-м пункте назначения;

­ затраты на транспортировку единицы груза из i-го пункта

отправления в j-й пункт назначения;

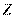­ совокупные затраты на перевозку всего груза;

­ исходно неизвестное количество груза, которое перевозится из

i-го пункта отправления в j-й пункт назначения.

Экономико-математическая модель задачи представлена формулами (2.100)÷(2.103):

(2.100)

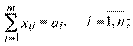(2.101)

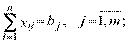(2.102)

(2.103)

Целевая функция (2.100) минимизирует совокупные затраты на транспортировку всех партий грузов из всех пунктов отправления во все пункты назначения. Система ограничений (2.101) говорит о том, что весь груз из каждого пункта его сосредоточения должен быть вывезен. Система ограничений (2.102) говорит о том, что потребность в грузе в каждом пункте назначения должна быть удовлетворена. Система ограничений (2.103) говорит о том, что по любому маршруту некоторое количество груза либо перевозится, либо нет.

Транспортная задача является задачей линейного программирования с (n + m) ограничениями ­ уравнениями и (n x m) неизвестными.

Транспортная задача, у которой суммарное наличие груза совпадает с суммарной потребностью, т.е. выполняется равенство (2.104)

(2.104)

называется закрытой (сбалансированной) транспортной задачей. Если условие (2.104) выполняется, то доказано, что транспортная задача имеет оптимальное допустимое решение. В случае если условие (2.104) не выполняется, то транспортная задача называется открытой. Решение транспортных задач с открытой моделью сводится к решению задач с закрытой моделью путем добавления фиктивного поставщика или фиктивного потребителя так, чтобы выполнялось условие (2.104). Транспортная задача относится к задачам распределительного типа и решается симплексным методом. Приведем прием решения транспортной задачи с помощью средства «Поиск решения» EXCEL.

Пример 2.4. Условия транспортной задачи представлены в таблице 2.6.

Таблица 2.6

В примере однородный груз должен быть доставлен от четырех поставщиков (n=4) четырем потребителям (m=4). Мощности поставщиков ( ) и потребность в этом грузе в каждом пункте назначения ( 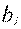) приведены в таблице 2.6. В левых нижних углах каждой клетки рабочей таблицы, которые соответствуют всем возможным путям перевозки груза из всех пунктов отправления во все пункты назначения, указаны затраты на транспортировку единицы груза по данному маршруту ( ). Суммарные запасы груза (550) и потребности в грузе (550) совпадают, значит это закрытая транспортная задача. Требуется составить план перевозок, обеспечивающий минимальные затраты на транспортировку всего груза.