Модели оптимизации раскроя промышленных материалов

В промышленном производстве в процессе подготовки производства часто различные исходные материалы подвергаются разрезке на заготовки меньших размеров. Материалы могут быть в виде прутков, труб, листов. Раскрой материалов (из металла, картона, бумаги, фанеры, древесины и т.п.) может производиться где угодно: в заготовительных участках цехов предприятий, мастерских и других производствах. В процессе раскроя неизбежны отходы из-за некратности размеров заготовки размерам исходного материала; по этой причине имеются значительные потери материалов в виде отходов.

Свести отходы к минимуму позволяет применение принципов линейного программирования в виде планирования "совместных раскроев".

Совместный раскрой предполагает, что заранее разрабатывается ряд возможных вариантов разрезки материала определенного размера на произвольные комбинации различных заготовок. Каждый такой вариант характеризуется различным составом заготовок, выкраиваемых из единицы материала, и разной величиной отходов. В этих вариантах не учтено условие комплектности. Для удовлетворения требования комплектности уровни возможного использования этих вариантов принимаются за переменные, а затем методами линейного программирования решается задача с учетом условия комплектности заготовок. Рассмотрим типовую задачу на оптимизацию раскроя.

Пример 2.3.Снабженческо-сбытовая фирма получает от поставщиков прутки стального проката длиной 600см. Согласно заявкам потребителей, требуются заготовки трех видов в следующих количествах: 150 тыс.шт. длиной 250см., 140 тыс.шт. длиной 190см. и 48 тыс.шт. длиной 100см. Сформулируем модель задачи оптимального раскроя с минимумом отходов. Наиболее трудоемкий этап в процессе построения модели рассматриваемой задачи заключается в определении всех возможных вариантов раскроя. В таблице 2.5 перечислены варианты раскроя одного прутка и размер отхода, полученного при раскрое одного прутка по каждому варианту (в см):

Таблица 2.5

Пусть x₁, x₂, x₃, x₄, x₅, x₆, x₇ ­ количество прутков, раскраиваемых по каждому варианту. Ниже приведена математическая модель задачи в виде выражений (2.89)÷(2.93):

целевая функция на минимум отходов:

, (2.89)

ограничения по условиям комплектности

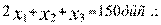(2.90)

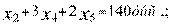(2.91)

(2.92)

условие неотрицательности

х_i ≥ 0; (2.93)

Для построения экономико-математической модели задачи примем следующие обозначения:

i – индекс вида заготовки ( );

j – индекс варианта раскроя ( );

A_i- требуемое количество заготовок i – го вида, необходимое для комплектности;

a_ij – количество заготовок i-го вида при раскрое единицы исходного материала по j-му варианту;

c_j –длина отхода при раскрое по j-му варианту.

Требуется определить x_j – количество прутков, раскраиваемых по j-му варианту. Формализованный вид экономико-математической модели представлен выражениями (2.94)÷(2.97):

целевая функция по критерию минимум отходов имеет вид:

, (2.94)

а по критерию минимума раскраиваемых единиц исходного материала

(2.95)

при условиях:

( ); (2.96)

. (2.97)

Получилась обычная задача линейного программирования, которую можно дополнить требованием целочисленности величины x_j . Во многих случаях, решения задач с обеими указанными целевыми функциями совпадают.

При определении возможных вариантов раскроя необходимо учитывать ряд условий: пусть L ─ длина раскраиваемого материала, а l_i ─ длина заготовки i-го вида, тогда признак полноценности варианта раскроя представлен соотношением (2.98):

(2.98)

а длина отхода для любого варианта раскроя должна быть меньше длины самой короткой заготовки:

(2.99)

Рассмотренная задача предусматривает раскрой длинномерных материалов (прутков, труб, профильного проката и др.). На практике приходится вести раскрой как рулонного, так и листового материала.

Для экономико-математической модели задачи раскроя рулонного материала изменится экономический смысл ряда обозначений:

a_ij ─ количество полос i-го размера, раскраиваемых из рулона по j-му

варианту раскроя;

c_j ─ размер краевого отхода при раскрое рулона по j-му варианту;

A_i ─ общее количество полос i-го размера, которое нужно получить при раскрое.

Решения задач оптимизации промышленных смесей и раскроя, представленных моделями (2.68÷ 2.72), (2.79÷2.83) и (2.94÷ 2.97) производится по программе алгоритма симплексного метода.

Вопросы по теме

1. Виды моделей оптимизации состава промышленных смесей.

2. Понятие плана совместного раскроя.

3. Как удовлетворяется требование комплектности раскраиваемых материалов.

4. Приведите выражения, отражающие условия.

5. Составьте модель задачи раскроя листового материала.