Экономико-математические модели оптимизации портфеля ценных бумаг

При формировании портфеля возможны три основные формулировки задач оптимизации:

1. целевая функция – максимизация доходности, остальное – в ограничения;

2. целевая функция – минимизация риска, остальное – в ограничения;

3. двухмерная оптимизация по параметрам “доходность-надежность” c последующим получением некоторого приемлемого значения комбинации "доходность – риск".

Одним из ограничений в этих моделях может быть ликвидность портфеля ценных бумаг на случай непредусмотренной ранее необходимости срочного расформирования всего портфеля. Уровень ликвидности определяется как число дней, необходимых для полной конвертации всех активов портфеля в денежные средства и перевода их на счет клиента.

Для получения количественных характеристик портфеля используются следующие зависимости:

Доходность портфеля рассчитывается как средневзвешенная доходность его составляющих:

, (2.107)

где:

x_i доля инвестиций, помещенных в i-ый актив (портфельный вес i-го актива),

d_i – ожидаемая ставка дохода по i-му активу,

n – число активов в портфеле.

Риск портфеля δ_p определяется как стандартное отклонение доходности по портфелю (δ_p ² - дисперсия доходности)

(2.108)

где

δ_i ─ стандартное отклонение доходности по i-активу,

r_ij ─ коэффициент корреляции доходностей i-го и j-го активов.

Варьируя портфельные веса x_i применяемых в составе портфеля активов, можно добиться оптимального, с точки зрения применяемого типа, портфеля.

Модель портфеля максимальной доходностипредставлена формулами (2.104)÷(2.111):

целевая функция:

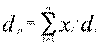max (2.104)

при ограничениях:

­ риск портфеля не должен превышать заданной величины

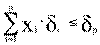(2.110)

­ все средства должны быть полностью инвестированы:

(2.111)

Модель портфеля минимального риска представлена формулами (2.112)÷(2.114):

целевая функция:

min (2.112)

при ограничениях:

­ доходность портфеля должна быть не меньше заданной величины

(2.113)

­ все средства должны быть полностью инвестированы:

(2.114)

В результате решения этих задач находятся доли капитала xi , эффективного портфеля.

Если x_i > 0, то это означает, что инвестор должен вложить x_i долю своего капитала в i-вид ценных бумаг.

Если же x_i < 0, то инвестору следует взять в долг ценные бумаги i-го вида на сумму, равную x_i долей своего капитала. Если взятие в долг невозможно, то в задачу следует ввести дополнительное ограничение:

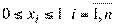(2.115).

Для решения задач с дополнительным условием неотрицательности переменных и без него разработаны пакеты прикладных программ, но можно использовать и возможности электронной таблицы EXCEL.

Вопросы по теме

1. Дайте определение портфеля ценных бумаг (ПЦБ).

2. Понятие структуры ПЦБ.

3. Как оценивается качество ПЦБ.

4. Понятие диверсификации ПЦБ.

5. Способы оценки доходности финансовых активов.

6. Возможные модели оптимизации ПЦБ и составляющие моделей.