
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модели оптимизации состава промышленных смесей.
В ряде производств (металлургической, пищевой, нефтеперерабатывающей отраслях промышленности) готовая продукция получается путем смешивания различных исходных компонентов (сырья), при этом качество готовой продукции должно соответствовать определенным требованиям при достижении максимального экономического эффекта.
Проблема рационального использования сырья в этих случаях может быть решена путем применения экономико-математических моделей оптимального составления смесей.
Как правило, исходные компоненты смеси взаимозаменяемы по содержанию качественных характеристик. При этом важно обеспечить соответствие готовой продукции по указанным качественным характеристикам необходимым требованиям, которые определяются стандартами и сертификатами.
Модель задачи позволяет найти такой набор компонентов смесей и их количественное соотношение, которое удовлетворяет заданным технологическим требованиям по качеству, а также требованиям принятого критерия (минимальной себестоимости или максимальной прибыли).
Задача смешивания может быть рассмотрена в натуральных единицах или в долях.
Рассмотрим задачу определения количества сырья, необходимого для получения смеси заданного объема.
На предприятии изготавливается бензин А-76, в котором содержание серы не более 0,3%, а октановое число должно быть не ниже 76.
Данные об используемых компонентах (видах сырья ─ нефтепродуктах) приведены в таблице 2.3. Требуется определить, сколько тонн каждого компонента нужно взять для получения 1000 т бензина А-76, чтобы при этом себестоимость бензина была минимальной.
Таблица 2.3
| Показатель | Компоненты автомобильного бензина (нефтепродукты) | |||
| Октановое число | ||||
| Содержание серы, % | 0,35 | 0,35 | 0,3 | 0,2 |
| Ресурсы, т | ||||
| Себестоимость (ден.ед.) |
Пусть  ─ оптимальные количества соответствующих компонентов, входящих в состав готовой смеси.
─ оптимальные количества соответствующих компонентов, входящих в состав готовой смеси.
Математическая модель задачи представлена в (2.62)÷(2.67):
целевая функция:
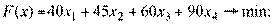 (2.62)
(2.62)
ограничение по октановому числу:
 ; (2.63)
; (2.63)
ограничение по содержанию серы:
 ; (2.64)
; (2.64)
ограничение по объему готовой продукции:
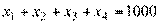 ; (2.65)
; (2.65)
ограничение по имеющимся ресурсам:
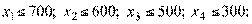 (2.66)
(2.66)
условие неотрицательности переменных:
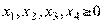 (2.67)
(2.67)
В общем виде задача формализуется следующим образом:

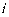 – индекс качественной характеристики; имеет отношение к исходным видам сырья, материалов и к готовой продукции (
– индекс качественной характеристики; имеет отношение к исходным видам сырья, материалов и к готовой продукции ( 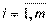 );
);
 - индекс исходных компонентов смеси (
- индекс исходных компонентов смеси (  );
);
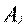 ─ имеющийся объем
─ имеющийся объем  -ой компоненты (сырья);
-ой компоненты (сырья);
 - содержание
- содержание 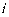 -той качественной характеристики в единице
-той качественной характеристики в единице  -го исходного компонента;
-го исходного компонента;
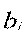 - содержание
- содержание 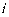 -той качественной характеристики в единице готовой смеси; для
-той качественной характеристики в единице готовой смеси; для  качественных характеристик, ухудшающих качество продукции, задается верхняя граница содержания той или иной качественной характеристики, а для
качественных характеристик, ухудшающих качество продукции, задается верхняя граница содержания той или иной качественной характеристики, а для  качественных характеристик, улучшающих качество продукции, задается нижняя граница содержания той или иной качественной характеристики;
качественных характеристик, улучшающих качество продукции, задается нижняя граница содержания той или иной качественной характеристики;
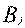 ─ имеющийся ресурс
─ имеющийся ресурс  -ой компоненты;
-ой компоненты;
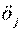 - цена единицы
- цена единицы  - ой исходной компоненты (включая расходы на переработку);
- ой исходной компоненты (включая расходы на переработку);
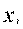 - количество
- количество  - ой исходной компоненты, которое входит в готовую смесь.
- ой исходной компоненты, которое входит в готовую смесь.
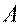 ─ общее количество готовой продукции, которое следует изготовить по плану.
─ общее количество готовой продукции, которое следует изготовить по плану.
Формализованная модель задачи оптимизации состава требуемого объема смеси представлена в (2.68) ÷ (2.72)
Целевая функция:
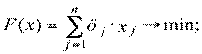 (2.68)
(2.68)
ограничения, ухудшающие качества:
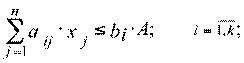 (2.69)
(2.69)
ограничения, улучшающие качества:
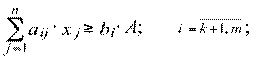 (2.70)
(2.70)
ограничение по плану производства продукции:
 (2.71)
(2.71)
ограничение по ресурсам:
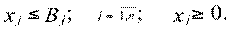 (2.72)
(2.72)
Вторая разновидность смесевых задач касается оптимизации структуры готовой продукции, безотносительно к объемам. Рассмотрим пример такой задачи.
Пример 2.2. Пусть требуется изготовить некоторую единицу объема сплава, содержащего не менее 4% никеля, не более 75% железа и 20% прочих веществ. Известна стоимость различных видов сырья и процентное содержание в них соответствующих элементов (табл. 2.4)
Таблица 2.4
| Вещество | Содержание элементов для каждого вида сырья, % | ||
| Железо | |||
| Никель | |||
| Прочие | |||
| Стоимость единицы сырья (ден.ед.) |
Определить оптимальную структуру сплава, при которой стоимость единицы сплава будет минимальной.
Математическая модель задачи:
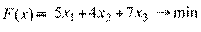 (2.73)
(2.73)
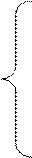
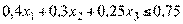 ; (2.74)
; (2.74)
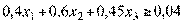 ; (2.75)
; (2.75)
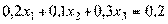 (2.76)
(2.76)
 ; (2.77)
; (2.77)
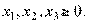 (2.78)
(2.78)
Экономико-математическая модель этой задачи будет включать выражения:
целевая функция:
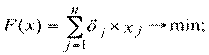 (2.79)
(2.79)
ограничения на качество смеси:
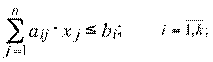 (2.80)
(2.80)
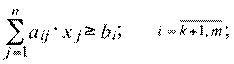 (2.81)
(2.81)
ограничение по формированию структуры смеси:
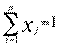 . (2.82)
. (2.82)
неотрицательность переменных:
 . (2.83)
. (2.83)
В данной задаче минимизируется стоимость единицы (кг, т и т.д.) смеси. Очевидно, что при любых объемах переработки сырья и выпуска готовой продукции, оптимальному плану будет соответствовать одна и та же структура смеси, т.е. соотношение в ней отдельных составных частей видов сырья.
Модели общего вида применяются при решении “задач о диете” – а именно задач составления оптимальных кормовых рационов, задач составления смесей минеральных удобрений, задач составления смесей нескольких химических веществ.
Более сложные модели задач смешивания составляются в тех случаях, когда в результате смешивания одних и тех же исходных компонентов могут быть получены различные виды готовой продукции. Тогда наряду с ограничениями по исходным компонентам задаются объемные ограничения по выпуску готовой продукции. Типичным примером таких моделей является модель смешивания нефтепродуктов. Рассмотрим пример постановки задачи смешивания нефтепродуктов.
Для получения готовых бензинов на установку поступают различные исходные компоненты (нефтепродукты). Оптимальный план позволяет определить, в каких количествах должны смешиваться различные исходные компоненты, чтобы различные сорта бензина (готовой продукции) выпускались в соответствии с планом и заданными по стандарту качественными характеристиками при обеспечении рентабельной работы установки.
Введем обозначения:
 - индекс качественной характеристики, применяется по отношению к исходным нефтепродуктам и к сортам бензина;
- индекс качественной характеристики, применяется по отношению к исходным нефтепродуктам и к сортам бензина;
 - индекс исходного нефтепродукта;
- индекс исходного нефтепродукта;
k –индекс вида готового бензина, 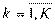 ;
;
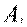 - ограниченное количество j-го вида исходного нефтепродукта;
- ограниченное количество j-го вида исходного нефтепродукта;
Bk – плановое задание по выпуску бензина k-го сорта,
hij – содержание i – той качественной характеристики в единице j – го исходного нефтепродукта;
Hik – содержание i - той качественной характеристики в бензине k- го вида;
Cj – цена исходного j- го нефтепродукта;
 – цена бензина k - го вида.
– цена бензина k - го вида.
Требуется определить Xjk – количество j–го вида исходного нефтепродукта, направляемое на получение k- го вида бензина.
Модель задачи представлена в выражениях (2.84)÷(2.88):

 (2.84)
(2.84)
по объему ресурсов: 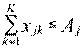 (
(  ), (2.85)
), (2.85)
по выпуску продукции: 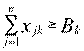 (
( 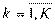 ), (2.86)
), (2.86)
по качественным характеристикам:
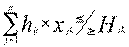 (
(  ;
; 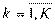 ) (2.87)
) (2.87)
 (
(  ;
; 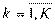 ). (2.88)
). (2.88)
Все сформулированные смесевые задачи решаются методами линейного программирования.
Дата добавления: 2014-11-13; просмотров: 840; Мы поможем в написании вашей работы!; Нарушение авторских прав |