Общая структура оптимизационной модели и система обозначений.

Основными элементами оптимизационной модели являются параметры и переменные. При этом параметры (исходные данные) – заранее известные фиксированные факторы, на значения которых исследователь не влияет, а значения переменных на момент постановки задачи неизвестны, изменение значений переменных приближает к достижению поставленной цели и получению решений задачи.

Указанные элементы оптимизационной модели связаны математическими зависимостями в виде составных частей оптимизационной модели, в качестве которых выступают критерий оптимальности и система ограничений. С точки зрения структуры оптимизационной модели критерий оптимальности – это показатель, на основании которого сравнивают эффективность управленческих решений в процессе выбора наилучшего из них. Формализованное или математическое выражение критерия оптимальности называется целевой функцией. Система ограничений составляется в виде уравнений (неравенств) и определяет область допустимых решений, то есть область, в пределах которой осуществляется выбор решений.

Построение экономико-математической модели оптимизационной задачи включает:

выбор некоторого числа переменных величин (экономических показателей) для формализации модели объекта;

информационную базу данных объекта;

выражение целевой функции как математическое представление критерия оптимальности через отобранные экономические показатели, с обозначением экстремума целевой функции (максимум или минимум);

представление системы ограничений математически в виде уравнений, неравенств через другие экономические показатели.

Необходимо отметить, что одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.

Методика построения экономико-математических моделей состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения.

Все условия задачи необходимо записать в виде уравнений или неравенств. В первую очередь необходимо определить систему переменных величин, которые для конкретной задачи могут обозначать искомый объем производства продукции на предприятии, количество перевозимого груза определенным потребителям и т.д. Как правило, для обозначения переменных величин используются буквы: x, y, z, а также их модификации. Например, модификации переменной x: x₁, x₂, x_n и т.д.

Переменные x1, x2, …., xn могут обозначать объемы производства продукции соответственно первого, второго и так далее n-го вида. Переменная 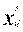может обозначать объемы производства j-го вида продукции на i-ом виде оборудования по s-му технологическому способу.

Для индексации, как правило, используются латинские буквы: i, j, s, l. Количество значений переменных может обозначаться буквами n, k, m. По каждой переменной для конкретной задачи дается словесное пояснение.

Целевую функцию задачи чаще обозначают буквами f, F, Z. Постоянные величины (нормы затрат ресурсов, цена или прибыль от единицы продукции и др.) обычно обозначают буквами: a, b, c, d и т.д.

Математическую модель задачи можно представить в виде:

найти значения переменных x₁, x₂,…., x_n, которые максимизируют или минимизируют целевую функцию

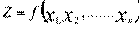(1.1)

и удовлетворяют системе из m ограничений

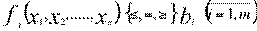. (1.2)

Если на переменные накладываются условие неотрицательности, тогда в модель задачи вводится условие

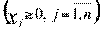. (1.3)

Иногда на переменные налагается условие целочисленности, тогда его можно записать в виде

x_j = 0, или 1, или 2, или 3 и т.д.

Если ограничения (1.2) и целевая функция (1.1) линейны относительно переменных, то модель называется линейной. В случае если хотя бы одна из функций (1.2) или Z нелинейна, то модель называется нелинейной.

Модель общей задачи линейного программирования применяют для решения задач определения оптимального плана выпуска продукции, оптимального использования производственных мощностей, сырья и других задач. В каждой из них отыскивается оптимум целевой функции при линейных ограничениях.

Задачи оптимизации решаются путём применения оптимизационных моделей методами линейного программирования.

Вопросы по теме.

1. Различие между параметрами и переменными в оптимизационной модели.

2. Назовите составные части оптимизационной модели.

3. В чем различие между понятиями критерий оптимальности и целевая функция.

4. Представьте запись общей модели оптимизационной задачи.

5. Приведите пример, подтверждающий, что одной системе ограничений может соответствовать несколько критериев оптимальности.