Вычисление объемов тел вращения.

Р
ассмотрим тело, образованное вращением вокруг оси криволинейной трапеции , ограниченной графиком неотрицательной непрерывной функции , ,осью абсцисс и отрезками прямых (рис. 10.2).
Р
азобьем отрезок точками на частей равной длины. На каждом из отрезков , выберем некоторую точку и составим интегральную сумму:
, (10.6)
где . Каждый член полученной суммы равен объему кругового цилиндра, а вся сумма равна объему соответствующего ступенчатого тела. Для непрерывной функции ,предел интегральных сумм (10.6) при n→∞ существует и равен объему Vрассматриваемого тела вращения:
.

Вычисление длин дуг плоских кривых.
П усть дана плоская кривая (рис. 10.1), уравнение которой , , где — непрерывно дифференцируемая функция на отрезке . Разобьем отрезок точками , на частей равной длины. Через точки деления проведем прямые, параллельные оси ординат . Точки пересечения этих прямых с кривой обозначим через . Соединив эти точки хордами, получим ломаную , вписанную в кривую . Пусть периметр этой ломаной равен . Длиной дуги будем называть число , равное пределу последовательности периметров :

Выведем формулу для вычисления длины дуги. Для этого сначала найдем периметр ломаной . Точка с координатами и и точка с координатами и являются концами го звена ломаной. Длину го звена вычислим по формуле расстояния между двумя точками плоскости:
. (10.3)
Учитывая, что – непрерывная дифференцируемая функция на отрезке ,по формуле Лагранжа имеем
, (10.4)
где — некоторая точка интервала . Подставив выражение (10.4) в формулу (10.3), получим:
, (10.5)
где . Значит, периметр ломаной равен следующей сумме:
.
Получили интегральную сумму для непрерывной функции на отрезке . Так как предел этой суммы при n → ∞существует, то согласно определению находим
.
Таким образом,

Вычисление площадей поверхностей тел вращения.
Найдем площадь поверхности, полученной в результате вращения кривой АВ вокруг оси абсцисс. Пусть функция ,непрерывно дифференцируема на отрезке . Через точки проведем прямые, параллельные оси ординат , а их точки пересечения с кривой обозначим через . Соединив эти точки хордами, получим ломаную .При ее вращении вокруг оси абсцисс получается поверхность, которая состоит из боковых поверхностей усеченных конусов, образованных вращением звеньев ломаной . Пусть площадь этой поверхности равна . Площадью поверхности тела вращениябудем называть число , равное пределу последовательности площадей :
.
Площадь поверхности, описанной ломаной выразится следующим образом:
, (10.7)
где мы воспользовались формулой (10.5). Сумма (10.7) не является интегральной суммой для функции
, (10.8)
так как в слагаемом, соответствующем отрезку 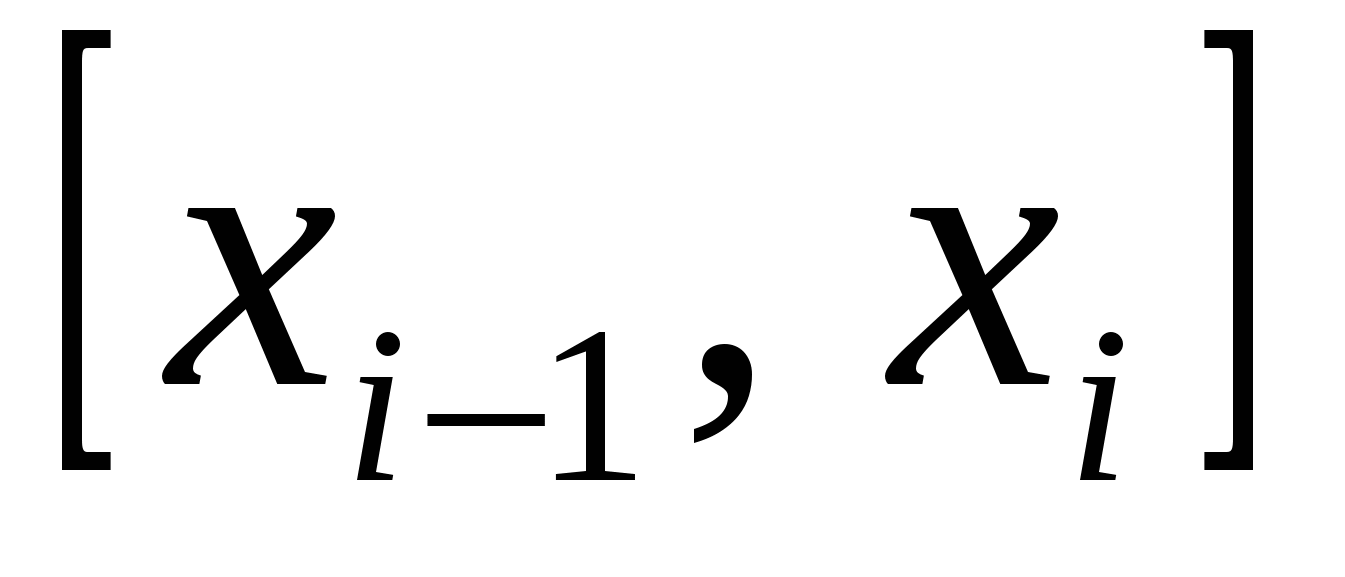,фигурируют несколько точек этого отрезка, а именно , , . Однако можно доказать, что предел суммы (10.7) равен пределу интегральной суммы для функции (10.8), т. е.


Таким образом,
.