Основные сведения. Основными уравнениями, позволяющими определять параметры напорных потоков жидкости при ее установившемся течении

Основными уравнениями, позволяющими определять параметры напорных потоков жидкости при ее установившемся течении, являются уравнение расхода и уравнение Бернулли.

Уравнение расхода, записанное для двух сечений (1 и 2) потока несжимаемой жидкости, представляет собой равенство объемных расходов и 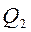в этих сечениях и имеет вид:

(1)

где: и – средние скорости в сечениях 1 и 2,

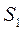и – площади этих сечений.

Отсюда следует, что величины средних скоростей в сечениях одного и того же потока обратно пропорциональны площадям этих сечений (для круглых сечений, обратно пропорциональны квадратам соответствующих диаметров).

Для потока сжимаемой жидкости уравнение (1), строго говоря, несправедливо и должно быть заменено уравнением весового или массового расхода .

Уравнение Бернулли так же записывается для двух живых сечений одного и того же потока (например, для сечений 1 и 2).

Для идеальной (невязкой) несжимаемой жидкости оно имеет вид:

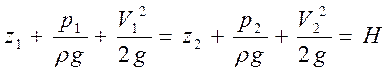. (2)

Каждый из членов уравнения Бернулли с одной стороны представляет собой некоторую высоту (напор), а с другой стороны является тем или иным видом удельной механической энергии жидкости.

Под удельной энергией жидкости в сечении понимается энергия, которой обладает единица веса жидкости (отнесенная к единице веса).

Таким образом, в уравнении (2):

– нивелирная высота, определяющаяся как расстояние от произвольно выбранной горизонтальной плоскости сравнения до центра тяжести рассматриваемого сечения, или удельная энергия положения жидкости в сечении;

– пьезометрическая высота (напор) или удельная энергия давления жидкости в сечении;

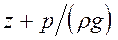– гидростатический напор, или удельная потенциальная энергия жидкости в сечении;

– скоростной напор (скоростная высота), или удельная кинетическая энергия жидкости в сечении;

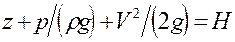– полный напор, или полная удельная механическая энергия жидкости в сечении данного потока, т.е. полный запас механической энергии, которым обладает единица веса жидкости в этом сечении.

Таким образом, энергетический смысл уравнения Бернулли для идеальной жидкости заключается в постоянстве полной удельной механической энергии жидкости вдоль данного потока.

Это уравнение, следовательно, выражает собой закон сохранения механической энергии в потоке движущейся идеальной жидкости. При этом различные виды удельной механической энергии жидкости могут в процессе движения преобразовываться из одного в другой, тогда как сумма их остается неизменной. Из уравнения также следует, что потенциальная энергия жидкости, в отличие от твердого тела, состоит из двух слагаемых, соотношение между которыми также может изменяться.

Для потока реальной (вязкой) жидкости уравнение Бернулли имеет несколько иной вид в связи с возникающей неравномерностью в распределении скоростей по сечению потока и наличием потерь энергии при движении жидкости, а именно:

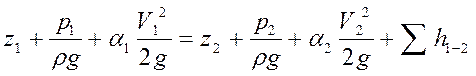(3)

где: – в отличие от уравнения (2), средние скорости в данном сечении;

– коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению;

– суммарная потеря напора на движение жидкости или потеря удельной механической энергии жидкости между рассматриваемыми сечениями.

Сумма трех членов 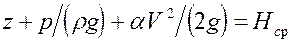представляет собой среднее значение полного напора или полной удельной механической энергии жидкости в данном сечении потока вязкой жидкости.

Следовательно, для потока реальной (вязкой) жидкости уравнение Бернулли является уравнением баланса удельной механической энергии жидкости с учетом потерь этой энергии, обусловленных вязкостью жидкости.

Местный полный напор в потоке H может быть определен с помощью, так называемой трубки полного напора, или трубки Пито, которая представляет собой трубку, изогнутую под прямым углом и установленную отверстием навстречу потоку (см. рис. 2). Если в том же сечении, где расположено приемное отверстие трубки Пито, установить пьезометр, то разность показаний этих двух трубок будет равна местному скоростному напору.

Рисунок 2 – Способ измерения местного скоростного напора

Так как все члены уравнения Бернулли в то же время представляют собой высоты (напоры), то это уравнение наглядно иллюстрируется графиком (см. рис. 3), на котором показаны изменение этих высот вдоль потока.

Кривая изменения пьезометрических высот называется пьезометрической линией; ее можно рассматривать как геометрическое место уровней жидкости в пьезометрах, установленных вдоль потока.

Кривая изменения величин полного напора вдоль потока называется линией полного напора, которую можно рассматривать как геометрическое место уровней жидкости в трубках Пито, установленных в центре соответствующих сечений вдоль потока. Для потока вязкой жидкости эта кривая вследствие потерь напора неуклонно спадает.

Рисунок 3 – Графическая иллюстрация уравнения Бернулли

Расстояние по вертикали между линией полного напора и пьезометрической линией представляет собой местный скоростной напор в данной точке сечения.