Вероятностные, числовые и интервальная характеристики результатов измерений.

Математическая статистика занимается как статистическим описанием результатов опытов или наблюдений, так и построением и проверкой подходящих математических моделей, содержащих понятие вероятности.

Событие является результатом любого опыта, проводимого в заданных условиях. Оно может иметь качественную или количественную характеристику. Качественной характеристикой события может быть, например изготовление качественной или некачественной детали, а количественной – случайная величина ее размера.

Событие, которое в результате данного опыта должно обязательно произойти называют достоверным, а то, которое в данных условиях не произойдет никогда, называют невозможным. Если в опыте событие может произойти, а может и не произойти, его называют случайным событием.

Вероятность P(A) – средняя частота появления случайного события А при многократной реализации условий для его наблюдения. Абсолютно достоверные события имеют P(A)=1, невозможные - P(A)= 0, для произвольного события 0<=P(A)<=1. вероятность наблюдения случайного события является его важнейшей характеристикой.

В большинстве случаев вероятность события не может быть найдена аналитически, ее оценивают на основании результатов опытов с помощью накопленной частоты случайного события W(A) – отношения числа опытов i, в которых появилось событие А, к общему числу проделанных опытов n, т.е. W(A)=i/n. Повторяя серию из n опытов многократно, будем получать различные значения W(A), однако, близкие к вероятности P(A) появления этого события. При этом, чем больше будет проделано опытов, тем ближе будет значение W(A) к P(A).

Если под событием понимать появление какого-либо числа, это будет случайной величиной.

Случайная величина – величина, наблюдаемое значение которой зависит от случайных причин. Характеризуется вероятностью, с которой она может приобрести то или иное значение из генеральной совокупности в области допустимых значений.

Генеральная совокупность – полный набор всех возможных значений случайной величины А. она м.б. или непрерывной средой, или набором дискретных значений. В статистике под генеральной совокупностью понимают все множество исследуемых объектов. Совокупность однородна, если хотя бы один ее существенный признак является общим для всех объектов совокупности.

Признак – качественная особенность объекта, принадлежащего данной совокупности. Признаки м.б. количественными и качественными(атрибутивными).

Наиболее полно случайные величины могут быть охарактеризованы с помощью интегральной функции распределения F(x), представляющей собой вероятность появления значения Х, не превышающего x, т.е.

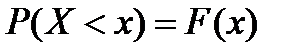
Функция распределения F(x) является неубывающей функцией Х. Вероятность попадания величины Х в интервал равна .

Функция F(x) удовлетворяет условиям и .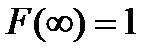

Для непрерывных, случайных величин F(x) имеет производную, которая называется функцией плотности вероятности . Плотность вероятности удовлетворяет условию .

Вероятность попадания случайной величины Х в интервал м.б. найдена через плотность вероятности .

Функция распределения данной случайной величины связана с ее плотностью вероятности соотношением , поэтому площадь под кривой равна единице, т.е. . (Вопрос 26 дополнительно)