Числовые характеристики

Характеристики центра распределения

В практических случаях вместо задания функций распределения случайной величины бывает достаточно указать некоторые их числовые характеристики, называемые статистиками.

В качестве числовых характеристик положения центра группирования случайных величин используют математическое ожидание а(для генеральной совокупности) или среднее арифметическое значение 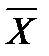(для группы случайных величин).

Математическое ожидание определяют как

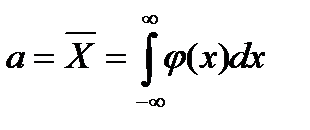
Это – основная, но не единственная характеристика центра группирования. Другими его характеристиками являются мода ( 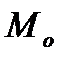) и медиана ( 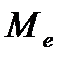). Модой величины Х является такое значение , в котором плотность вероятности имеет максимальное значение. Медианой величины Х служит значение , которое соответствует условию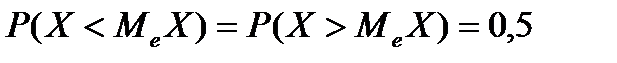

Геометрически медиана – абсцисса прямой, которая делит площадь ограниченную кривой плотности вероятности, пополам.

Для симметричных распределений характерно совпадение значений средней арифметической, моды и медианы. Если , то ряд будет иметь левостороннюю асимметрию, если - правостороннюю асимметрию. В умеренно асимметричных рядах соотношение между указанными показателями выражается следующим образом:

.

Характеристики рассеивания.

Одной из основных характеристик рассеивания случайной величины Х около центра распределения служит дисперсия, которая определяется по формуле:

Часто в качестве меры рассеивания случайной величины вместо дисперсии используют положительное значение квадратного корня из дисперсии, которое называется средним квадратическим отклонением или стандартным отклонением

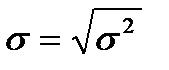
В практике также широко применяют характеристику рассеивания, называемую коэффициентом вариации, представляющим собой отношение СКО к мат.ожиданию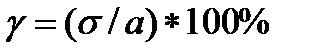

Коэффициент вариации показывает, насколько велико рассеивание по сравнению со средним значением случайной величины.

Моменты распределения.

Начальным моментом распределения k-го порядка называется число, определяемое по формуле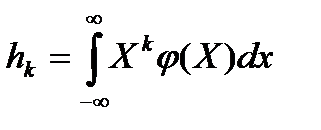

Центральный моментk-го порядка 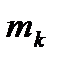определяется из выражения

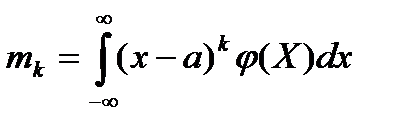
Для статистической обработки результатов используют моменты первых четырех порядков. Между начальным и центральным моментами распределения существуют следующие зависимости:

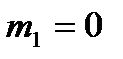
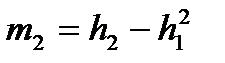
Здесь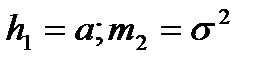

Третий центральный момент используют для вычисления показателя асимметрии распределения .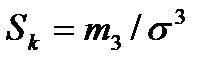

Четвертый центральный момент 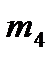используется для определения показателя эксцесса 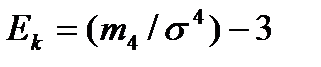, являющегося характеристикой крутизны распределения. Отличные от нуля показатели асимметрии и эксцесса указывают на отклонение рассматриваемого распределения от нормального.