Исследование стержневых систем на геометрическую неизменяемость

Строительная механика изучает методы расчета сооружений в целом на прочность, жесткость и устойчивость. Целью расчета сооружения является проверка его на прочность, жесткость и устойчивость.

Сооружение структурно или геометрически неизменяемо – изменение формы возможно лишь при деформации элементов сооружения, в противном случае сооружение называется геометрически изменяемым и такие не используются в строительстве.

В стержневую систему во все узлы вставляются шарниры – ферма.

Если элементы соединяются различными связями – рама.

Изменяемость самой структуры системы и подвижность системы, относительно основания определяется степенью свободы.

Степень свободы системы – число независимых геометрических параметров, определяющих положение всех элементов сооружения.

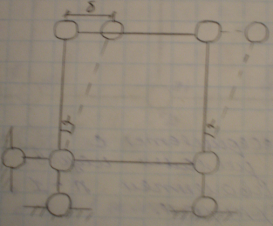
Чтобы обеспечить неподвижное основание необходимо 3 опорных стержня (min)/

Степень свободы W=1 – механизм геометрически неизменяемая система.

Шарнирно-подвижная опора – односвязная

Шарнирно-неподвижная – двухсвязная

Жесткая заделка – трехсвязная

Элементы системы соединяются между собой шарнирами или опорными стрержнями

Заведомо неизменяемая часть системы – диск.

Каждый диск имеет з степени свободы

Шарнир, соединяющий 2 диска эквивалентен двум связям. То есть он запрещает взаимное смещение, но не исключает возможного взаимного поворота.

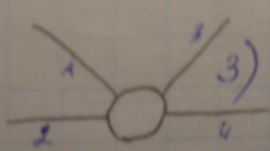
Каждый шарнир соединяет более двух дисков – кратный. Кратный шарнир эквивалентен n-1 простым

шарнирам, где n – число соедин. дисков.

Каждый опорный стержень накладывает 1 связь, то есть запрещающую перемещение диска в направлении этого опорного стержня

Кинематическая связь – когда всякое устройство отнимает 1 степень свободы.

Степень свободы системы:

W = 3D – 2Ш – Со(1) , где

D – число дисков;

Ш – число простых шарниров;

Cо – число опорных стержней;

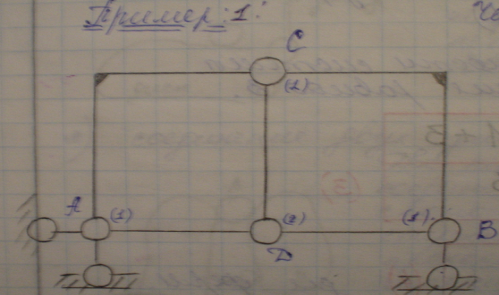
D=5; Ш=6; Со=3;(жесткая заделка)

Для определения числа D надо мысленно убрать все шарниры и опорные стержни. Для определения числа Ш надо мысленно убрать опорные стержни.

W=3*5-2*6-3=0 = эта система статически определима и может быть неизменна.

Степень свободы для ферм:

W = 2У - С - Со (2), где

У – число шарнирных узлов фермы;

С – число стержней фермы;

Со – число опорных стержней;

Для системы, не имеющей связи с основанием (Со=0) степень свободы складывается из 2-х частей:

1) степени изменяемости внутренней структуры системы(И)

2) степень подвижности системы относительно основания = 3.

W= И + 3; W = 3D – 2Ш – 3; (3)

W = 2У – С – 3; (4)

При использовании формул 1-4 может быть:

W > 0 (И>0) - система Г. И. = с ней нельзя работать

1) W = 0 (И=0) - система имеет min количество связей и может быть неизменяемой при этом она статически определена.

2) W < 0 (И<0) - система имеет лишние связи, то она может быть статически неопределимой = может быть неизменяемой.

3) W ≤ 0 (И≤0) - необходимое, но недостаточное условие геометрической неизменяемости системы.

Принципы образования структурно-неизменяемых систем.

1. Диада – шарнирный узел, присоединение двух шарниров и двух диад, то неизменяется степень свободы

2. Соединение 2 дисков. Две неизменненые фигуры соединены двух дисков с помощью шарнира и стержня, ось которого проходит через центр этого шарнира.

3. Пересечение из трех шарниров – получаем фиктивный шарнир

Условие геометрической неизменяемости

4. соединение 3-х дисков с помощью 3 шарниров, не лежащих на одной прямой.

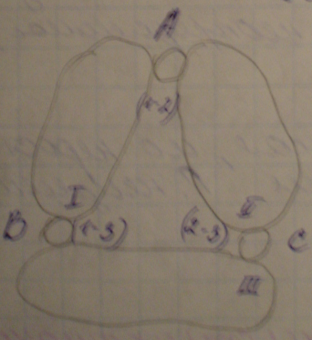
5. соединение 3-х дисков с помощью 6 стержней, не параллельных и не пересекающихся в одной точке

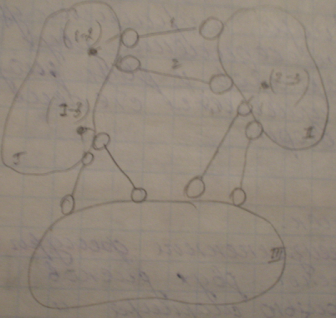
Аналитические методы исследования неизменяемости

1. Общий аналитический метод

Пусть имеем статически определимую ферму, имеющую n стержней с усилиями стержней X1,X2,…Xn

n – уравнений равновесия, которые можно записать в следующем виде:

, где а_ik – cos-ы составляющих углов при неизвестных условиях

y_ip – составляющие узловой нагрузки

Теория определителя по формуле Крамера: (1)

D – общий определитель составленный из коэффициентов а_ik

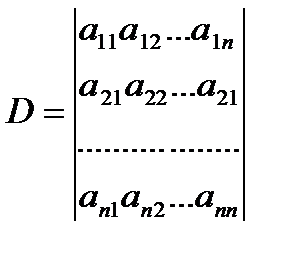
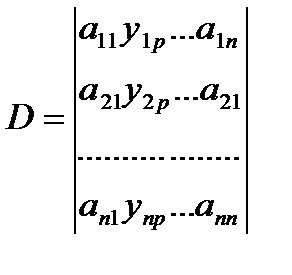
D_i – частный определитель, отражающий влияние узловой нагрузки. Он получается из общего заменой i-го столбца столбцом свободных членов y_ip

Формула (1) позволит провести анализ неизменяемости ферм:

1) D_i ≠ 0, D ≠ 0 – все усилия Х имеют (получают) конечные определенные значения и ферма неизменяема;

2) D_i ≠ 0, есть нагрузка узла;

D = 0 – Х_i = D_i/0 = ∞

Система мгновенна изменяема

3) D_i = 0 - нагрузки нет;

D = 0 X_i = 0/0 - мгновенно изменяемая система;

2. Способ нулевой нагрузки

Суть метода: если при действии нагрузки все усилия Х в стержнях имеют конечные и определенные значения, то при нулевой нагрузкевсе усилия в стержнях должны быть нулевыми.

3. Способ замены стержней

Применяется или используется в сложных фермах (3 или более стержней используется)