
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет статически неопределенных систем методом перемещений. Степень кинематической неопределимости, основная система
Разность между числом искомых неизвестных усилий и независимых уравнений равновесия определяет степень статической неопределимости системы. Степень статической неопределимости всегда равна числу избыточных (лишних) связей, удаление которых превращает статически неопределимую систему в статически определимую геометрически неизменяемую систему. Избыточными могут быть как внешние (опорные) связи, так и внутренние, накладывающие определенные ограничения на перемещение сечений системы друг относительно друга. Стат неопред системы можно рассчитывать двумя методами: Метод сил и метод перемещений.  Суть метода: Вначале определяют перемещения узлов рамы, а затем находятся внутренние усилия в элементах рамы, соответствующие найденным перемещениям. При определении линейных и угловых перемещений все элементы рамы считаются нерастяжимыми и не сжимающими (т.е. пренебрегают продольными силами).
Суть метода: Вначале определяют перемещения узлов рамы, а затем находятся внутренние усилия в элементах рамы, соответствующие найденным перемещениям. При определении линейных и угловых перемещений все элементы рамы считаются нерастяжимыми и не сжимающими (т.е. пренебрегают продольными силами).
z1 – радианы
z2 – метры
В результате смещения узлы рамы получают как линейные так и угловые перемещения
Переход из недеформированного состояния в деформированное можно показать следующим образом:
 Переход из начального деформированного состояния состоит из 5 позиций
Переход из начального деформированного состояния состоит из 5 позиций
Поступательное перемещение всех точек стержня АВ параллельного первоначальному положению на величину ∆а, при этом стержень остался прямым = внутренних сил в стержне не возникает.
Перемещение одного из концов стержня по отношению к другому по нормали к оси на величину ∆ва.
Поворот левого конца стержня на φа.
Поворот правого конца стержня на φв.
Перемещение точек стержня от действия заданной нагрузки.
n – общее число неизвестных метода перемещений, определяется:
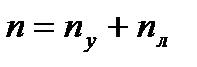 - Степень кинематической неопределимости
- Степень кинематической неопределимости
nу – число неизвестных угловых перемещений, nл – число независимх линейных перемещений узлов рамы, n – степень кинематической неопределимости
nу = числу жестких узлов рамы, кроме опорных W = 2У – С – Со – степень свободы (1)
У - число шарнирных узлов, С - число стержней фермы, С0 - число опорных стержней
W = 2*4 - 3 - 4 =1 nл = W
Основная система метода перемещений (ОСМП) образуется наложением на узлы сооружения связей, препятствующим их угловым и линейным перемещениям. Если число наложенных на узлы угловых и линейных связей совпадает со степенью кинематической неопределимости сооружения, то в основной системе метода перемещений все узлы будут неподвижными
 При выборе основной системы метода перемещений угловые связи накладываются на узлы сооружения и препятствуют только их поворотам. Такие связи называются «плавающими» заделками. Линейные связи, число которых определяется по формуле 1, на узлы накладываются так, чтобы шарнирная схема заданного сооружения была геометрически неизменяемой.
При выборе основной системы метода перемещений угловые связи накладываются на узлы сооружения и препятствуют только их поворотам. Такие связи называются «плавающими» заделками. Линейные связи, число которых определяется по формуле 1, на узлы накладываются так, чтобы шарнирная схема заданного сооружения была геометрически неизменяемой.
Основная система метода перемещений.
1 добавочная связь – плавающая заделка- односвязная опора запрещает угол поворота, оставляя возможность линейного смещения. (возникает реактивный момент)
2 добавочеая связь препятствует линейному смещению. (возникает реактивное усилие)
Т. О. система стала 4 раза статически неопределима
Основная система кинематически определима, т. к. все узлы стали подвижными.
R1 и R2 – реактивный момент и усилие.
Чтобы обратить R1 в нуль необходимо плавающую заделку повернуть на угол, равный действующему углу поворота. Чтобы обратить R2 в нуль нужно сместить узел 2 на величину = действующему смещению угла (величину z2). Если реакции обратим в нуль, то внутренние усилия будут одинаковые. Отрицание реакций в веденных связях – есть сущность канонических уравнений метода перемещений.
 - погонная жесткость
- погонная жесткость
Принцип независимости:

R1P – реакция первой связи, вызванная действием нагрузки (осталные от поворота и линейного смещения)

Принцип пропорциональности:
 , где r11 – реакция 1 связи от поворота этой связи на угол z1 = 1.
, где r11 – реакция 1 связи от поворота этой связи на угол z1 = 1.
Реакции – правило знаков:
Реакции во введенной связи считается “+”, ее направление совпадает с выбранным направлением неизвестных перемещений.
Каноническое уравнение в развернутом виде:

Для определения реактивных моментов используют способ вырезания узлов. Для определения реактивных усилий – метод сечений.
Способы проверки. Окончательная эпюра моментов проверяется дважды статически (явл. необходимой, но недостаточной) и кинематически.
Статическая – любой узел рамы должен находиться в равновесии, т. е. сумма моментов любого узла =0.
Кинематическая – проверяется отсутствие перемещений по направлению неизвестных (отброшенных связей). Сколько неизвестных столько и проверок:
 1=
1=  ;
;  2=
2= 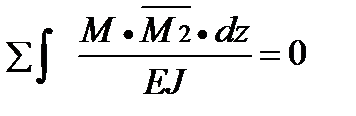
Можно сделать суммарную проверку, т.е. отсутствие перемещений по направлению сразу всех неизвестных:
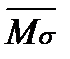 =М1+ М1+ М2+ М3
=М1+ М1+ М2+ М3
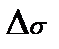 =
= 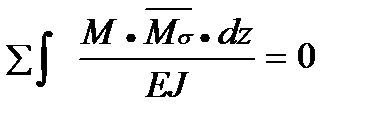
Дата добавления: 2015-04-18; просмотров: 481; Мы поможем в написании вашей работы!; Нарушение авторских прав |