
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие ферм, признаки их статической неопределимости, определимости, основные способы определения усилий в стержнях ферм.
Расчёт плоских ферм.
Ферма- стержневая система, у которой во всех узлах шарнирыи при этом она остаётся геометрически неизменяемой.
Степень статической неопределимости ферм : n=C+Cо-2У,
где У-число узлов фермы.С-число стержней. Со-число опорных стержней.
Определение степени свободы для ферм:W=2У-С-Со.
Основные способы определения усилий в стержнях ферм:
1)Способ моментных точек
2)Способ проекций
3)Способ вырезания узлов
Если невомзожен 1 способ то использ-ся 2,если же 2 способ неприменим , то используется 3 способ.
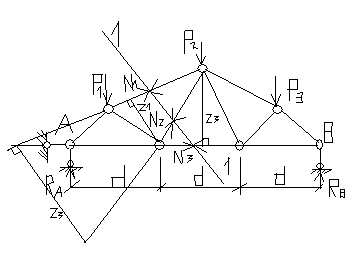 -способ моментных точек:
-способ моментных точек:
 СуммаМк1=-N1*r1-Ra*d+P1*d/2=0,отсюда находим N1.
СуммаМк1=-N1*r1-Ra*d+P1*d/2=0,отсюда находим N1.
-способ проекций(моментные точки в бесконечности)
суммаYлев=Ra+Nsina=0
Статически неопределимые стержневые системы, определение степени статической неопр-ти, св-ва статически неопределимых систем. Сущность метода сил. Основные способы проверки правильности построения эпюр.
Стержневые системы - системы, состоящие из отдельных , обычно прямолинейных, соединенных между собой в узлах с помощью сварки, заклепок, болтов и других скреплений; одним из таких видов систем являются плоские фермы.
При расчете статически неопределимых рам определяют реакции опорных связей и внутренних усилий. Они принимаются за неизвестные. Если уравнений статики недостаточно для определения этих неизвестных, то система статически неопределима.
Свойства стат. неопределимых систем:
- распределение усилий между элементами зависит от материала этих элементов и их размеров;
- изменение температуры, смещение опорных связей, неточность изготовления элементов и последующей сборки все это приводит к появлению дополнительных усилий и напряжений.
Расчет статически неопределимых систем начинают с определения статической неопределимости – это число лишних связей, удаление которых превращает заданную стат. неопределимую раму в стат. определимую и геометрически неизменяемую.
Для рам степень статической неопределимости:
n=3m – Ш , Ш – число простых шарниров (соединяет 2 стержня или 2 диска);

 m – число замкнутых контуров в системе в предположении отсутствия шарнирных соединений;
m – число замкнутых контуров в системе в предположении отсутствия шарнирных соединений;
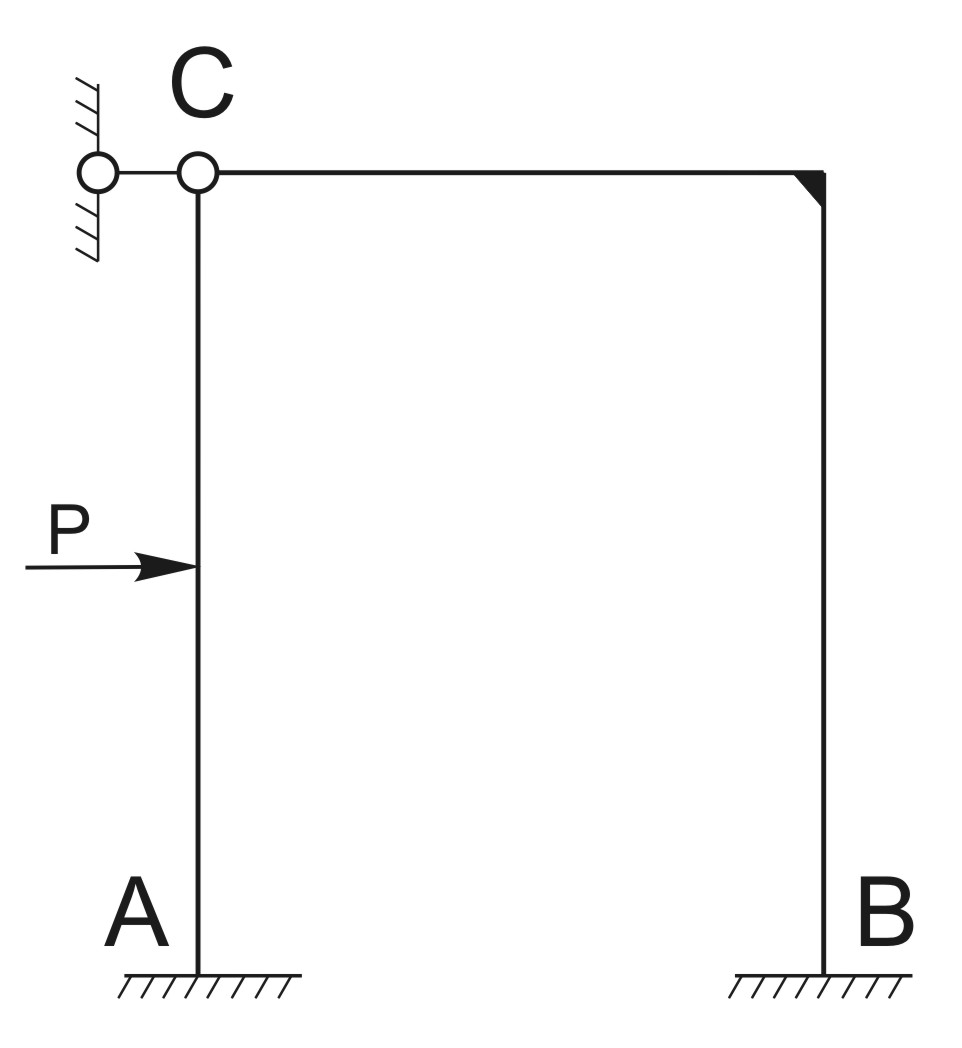
Задана стат. неопределимая рама. n=3*2 – 3 = 3 раза стат. неопределима.
Раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.
Основная система метода сил – это статически определимая и геометрически неизменяемая система, полученная из заданной системы удалением лишних связей.
После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы обозначают Xi-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы Xi, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.
Эквивалентная система – это основная система, загруженная реакциями отброшенных связей и заданной нагрузкой. Она д. б. тождественна заданной раме статически (внутр. силы одинаковы) и кинематически (перемещение точек д. б. одинаковыми)
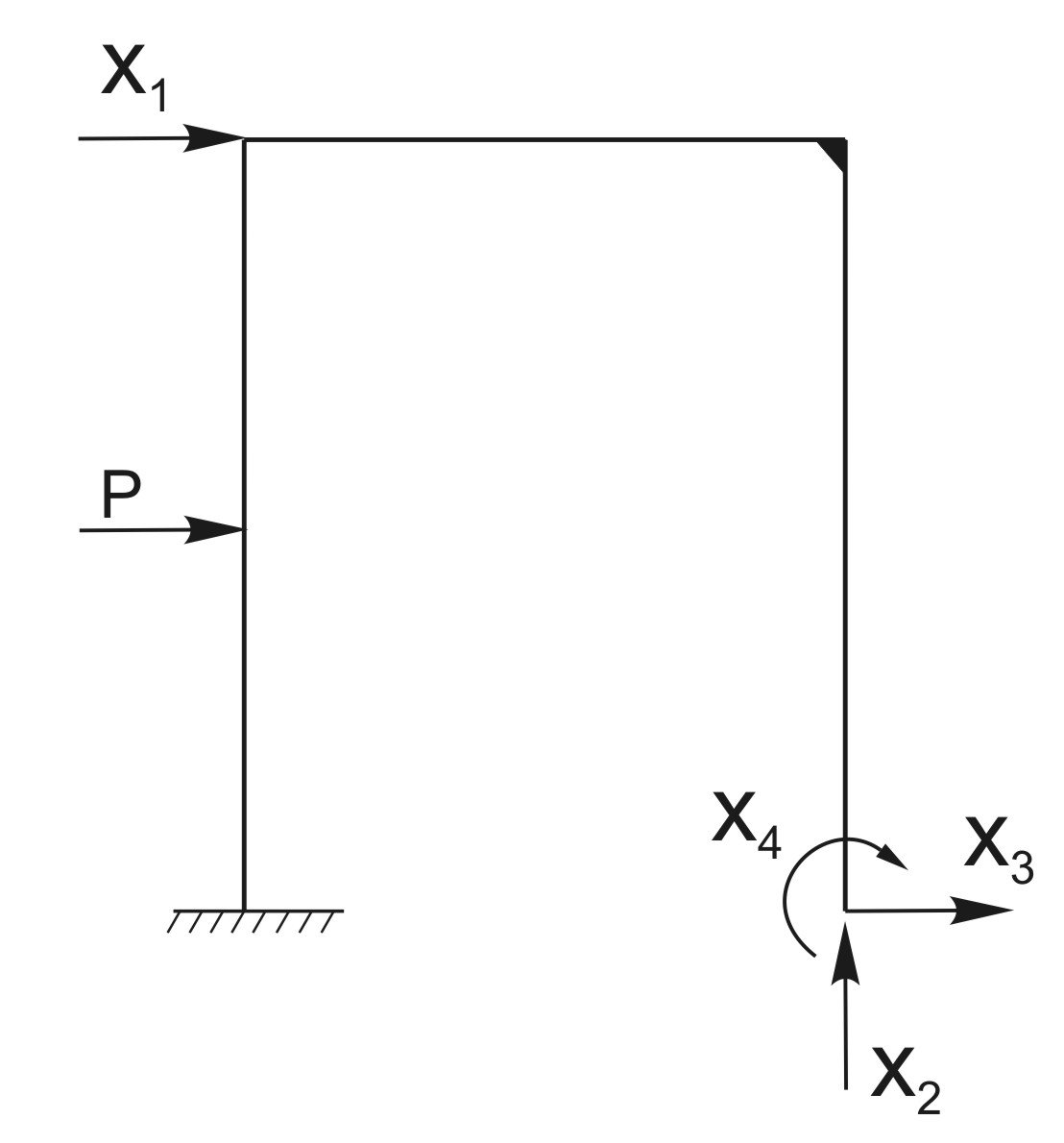 Теперь составим уравнения совместности перемещений:
Теперь составим уравнения совместности перемещений:
 1(x1,x2,x3,х4,Р)=0
1(x1,x2,x3,х4,Р)=0
 2(x1,x2,x3,х4,Р)=0 – первый индекс направление перемещения, второй – причина перемещения
2(x1,x2,x3,х4,Р)=0 – первый индекс направление перемещения, второй – причина перемещения
 3(x1,x2,x3,х4,Р)=0
3(x1,x2,x3,х4,Р)=0
 4(x1,x2,x3,х4,Р)=0
4(x1,x2,x3,х4,Р)=0
Применяем принцип независимости сил и их сложения:
 1(x1,x2,x3,х4,Р)=
1(x1,x2,x3,х4,Р)=  1(x1)+
1(x1)+  1(x2)+
1(x2)+  1(x3) +
1(x3) +  1(x4) +
1(x4) +  1(Р)=0
1(Р)=0
 1(x1)=
1(x1)=  11*x1 – принцип пропорциональности, где
11*x1 – принцип пропорциональности, где 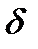 11 – перемещение по направлению x1, от действия x1=1;
11 – перемещение по направлению x1, от действия x1=1;  1(x2)=
1(x2)= 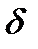 12*x2 и т. д.
12*x2 и т. д.
Записываем канонические уравнения метода сил. Число уравнений равно степени статич. неопределимости. Каждое уравнение это отрицание перемещений по направлению отброшенных связей.
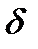 11 x1+
11 x1+ 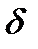 12 x2+
12 x2+ 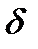 13 x3+
13 x3+ 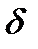 14 x4+
14 x4+  1(Р)=0 – канн. ур., отрицание перемещ. по направл. x1.
1(Р)=0 – канн. ур., отрицание перемещ. по направл. x1.
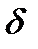 21 x1+
21 x1+ 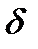 22 x2+
22 x2+ 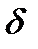 23 x3+
23 x3+ 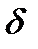 24 x4+
24 x4+  2(Р)=0
2(Р)=0
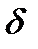 31 x1+
31 x1+ 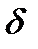 32 x2+
32 x2+ 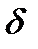 33 x3+
33 x3+ 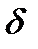 34 x4+
34 x4+  3(Р)=0
3(Р)=0
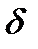 41 x1+
41 x1+ 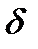 42 x2+
42 x2+ 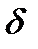 43 x3+
43 x3+ 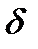 44 x4+
44 x4+  4(Р)=0
4(Р)=0
Далее решаем каноническое уравнение. Для этого основную систему загружаем по отдельности единичными неизвестными по отдельности и строим эпюра единичных изгибаемых моментов. Находим коэффициенты при неизвестных:
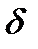 ik=
ik=  ;
;  i(Р)=
i(Р)= 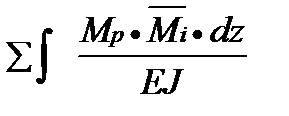
Строим эпюру изгибающих моментов для заданной рамы:
М=  Х1+
Х1+ 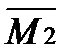 Х2+
Х2+ 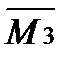 Х3+
Х3+ 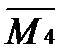 Х4+Мр
Х4+Мр
Способы проверки. Окончательная эпюра моментов проверяется дважды статически (явл. необходимой, но недостаточной) и кинематически.
Статическая – любой узел рамы должен находиться в равновесии, т. е. сумма моментов любого узла =0.
Кинематическая – проверяется отсутствие перемещений по направлению неизвестных (отброшенных связей). Сколько неизвестных столько и проверок:
 1=
1=  ;
;  2=
2= 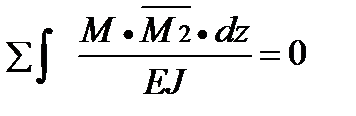
Можно сделать суммарную проверку, т.е. отсутствие перемещений по направлению сразу всех неизвестных:
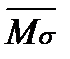 =М1+ М1+ М2+ М3;
=М1+ М1+ М2+ М3; 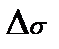 =
= 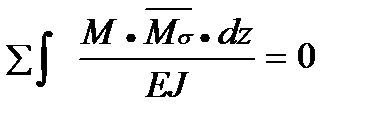
Дата добавления: 2015-04-18; просмотров: 1035; Мы поможем в написании вашей работы!; Нарушение авторских прав |