Отличия линейного и динамического программирования в математике.

Линейное программирование — это частный раздел опти мального программирования. В свою очередь оптимальное (математическое) программирование — раздел прикладной математики, изучающий задачи условной оптимизации. В экономике такие задачи возникают при практической реали зации принципа оптимальности в планировании и управлении.

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах 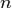-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Для принятия крупномасштабных плановых решений стратегического характера используются модели линейного программирования (ЛП). Линейное программирование относится к числу наиболее широко распространенных методов, применяемых для решения производственных и коммерческих задач.

Модель ЛП должна содержать целевую функцию и некоторую совокупность ограничений. Физический смысл целевой функции зависит от существа организационной задачи. В задачах производственно-экономического характера целевая функция чаще всего представляет собой прибыль (максимизация) или затраты (минимизация). Ограничения определяют область допустимых значений управляемых переменных, т.е. измеримых величин, значения которых подлежат оптимизации. Выраженные через управляемые переменные целевая функция и ограничения составляют модель организационного управления.

Существует несколько способов решения задачи ЛП, наиболее часто используют симплекс-метод.

Задачи оперативного управления относятся к числу микроэкономических задач управления. К задачам оперативного управления относят задачи:

● распределение ресурсов (разработка правил управления запасами, устанавливающих момент пополнения запасов и размер пополняющего заказа);

● управление запасами (определение необходимого объема запасных частей, гарантирующего эффективное использование дорогостоящего оборудования);

● разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию.

● распределение капитальных вложений между возможными новыми направлениями их использования.

● выбор методов проведения рекламной компании,

● систематизация методов поиска ценного вида ресурсов.

● составление календарных планов текущего и капитального ремонта сложного оборудования.

● разработка правил замены выбывающих из эксплуатации основных фондов.

Для решения таких задач широко используют методы динамического программирования (ДП). ДП - это математический аппарат, разработанный с целью повышения эффективности вычислений при решении задач математического программирования путём их разложения (декомпозиции) на относительно большие и, следовательно, менее сложные подзадачи.

Динамическое программирование в математике и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой (англ.), выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

Фундаментальным принципом, положенным в основу теории ДП, является принцип оптимальности: каким бы ни был путь достижения некоторого решения (состояния), последующие решения должны принадлежать оптимальной стратегии для части пути, начинающейся с этого состояния, т.е. каждом этапе оптимальная стратегия определяется независимо от стратегий, применённых на предыдущих этапах.

Однако динамическое программирование имеет и свои недостатки. В отличие от линейного программирования, в котором симплексный метод является универсальным, в динамическом программировании такого метода не существует.

Каждая задача имеет свои трудности, и в каждом случае необходимо найти

наиболее подходящую методику решения. Недостаток динамического программирования заключается также в трудоемкости решения многомерных задач. Задача динамического программирования должна удовлетворять два условия. Первое условие обычно называют условием отсутствия последействия, а второе –условием аддитивности целевой функции задачи.