Преобразование спектров сигналов в параметрических цепях.

(Баскаков 12.1)

Параметрическую цепь называют резистивной, коэффициент усиления зависит от времени:

Простейшей системой такого вида служит параметрический резистор с сопротивлением . Закон, связывающий мгновенные значения напряжения и тока в этом двухполюснике, таков:

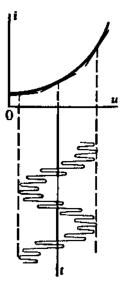
На практике параметрически управляемые резисторы создают следующим образом. На вход нелинейного двухполюсника подают сумму двух колебаний: управляющего напряжения и напряжения сигнала , при этом управляющее напряжение значительно превышает по амплитуде полезный сигнал. Ток в нелинейном двухполюснике можно записать как:

Обозначим через 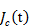приращение тока в двухполюснике, вызванное наличием сигнала, получим:

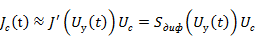
По рисунку видно, что амплитуда колебаний выходного тока (крутизна кривой) зависит от текущего уровня управляющего напряжения.

Преобразование частоты

Так называют трансформацию модулированного сигнала, связанную с переносом его спектра из окрестности несущей частоты в окрестность другой частоты 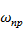, совершаемую без изменения закона модуляции.

Преобразователь частоты состоит из смесителя (параметрического элемента) и гетеродина — вспомогательного генератора гармонических колебаний с частотой , служащего для параметрического управления смесителем. Для смесителя:

Если на вход преобразователя действует АМ-сигнал , то выходной ток будет иметь вид:

В качестве новой принято выбирать частоту . Ток на новой частоте:

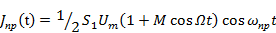
Получился тот же сигнал, но модулированный на новой частоте. Для выделения составляющих спектра с частотами, близкими к новой, используют колебательный контур, настроенный на эту частоту.