Метод деления отрезка пополам

Метод деления отрезка пополам (дихотомии) – задается интервал, в котором имеется корень (проверка наличия корня внутри интервала выполняется вычислением значений функции на его границах с последующей проверкой этих значений на разные знаки через операцию умножения – если произведение меньше нуль, то знаки на границах интервала разные). Затем интервал разбивается на два и выбирается тот, в котором остался корень. Процедура повторяется, пока интервал не станет меньше погрешности erf. Алгоритм метода показан на рис.7. Обычно всегда проверяется левый интервал, а после проверки выбирается необходимый. Ответом является середина последнего интервала. Для ускорения работы алгоритма можно проверять и попадание в сам корень, в этом случае произведение становится равным нулю, а корень оказывается на одной из границ интервала. Разберем данную процедуру на примере:

− задаем уравнение Y=f(X), погрешность вычисления и левую границу Х_л;

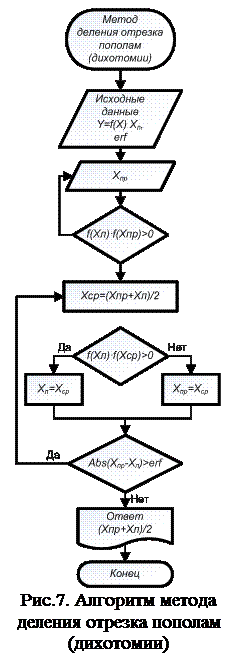− задаем правую границу Х_пр и проверяем произведения f(X_л)·f(X_пр).Если значение больше нуля повторяем ввод правой границы, если меньше переходим к реализации алгоритма, а если равен нулю, определяем границу, где найден корень;

− находим середину интервала Х_ср=(Х_пр+Х_л)/2 и проверяем значение произведения для левой половины f(X_л)·f(X_ср). Если значение равно нулю, то корень в средней точке, если значение меньше нулю, то левый интервал содержит корень и правую часть можно отбросить приравняв Х_пр= X_ср иначе корень находится в правой части и отбрасываем левую Х_л= X_ср;

− процедуру повторяем, пока (Х_пр-Х_л)>erf. Ответом является среднее значение найденного интервала.