Нейронные сети прямого распространения с дискретной функцией активации: архитектура, алгоритмы обучения, применение.

Искусственные нейронные сети, предназначенные для решения конкретных задач, могут содержать от нескольких нейронов до тысяч и даже миллионов элементов. Каждый отдельный искусственный нейрон (рис.1) имеет некоторое множество входов, на которые подаются компоненты х₁, ... х_n входных векторов или изображений и постоянный сигнал смещения x₀ º 1. Все входные сигналы суммируются с учетом весов w₀, w₁, ..., w_n связей нейрона:

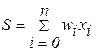а затем сигнал суммы воздействует на функцию активации нейрона. Простейшие нейроны обладают биполярной

или бинарной функцией активации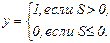

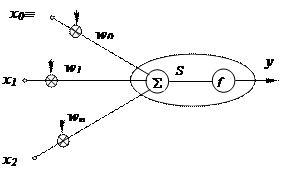Несмотря на простоту отдельного нейрона он может быть использован для решения ряда задач распознавания и классификации изображений. Поскольку выходной сигнал у двоичного нейрона принимает только два значения, то нейрон можно использовать для классификации предъявляемых изображений на два класса:

X¹ = {X¹¹, ..., X^1q}, X² = {X²¹, ..., X^2P}, X¹ È X² = M; X¹ Ç X = 0.

Пусть первому классу Х¹ соответствует выходной сигнал у =1, а классу Х² - сигнал у = -1. Если, например, предъявлено некоторое изображение Х^a = (Х^a₁, ..., Х^a_n), Х Î М и его взвешенная сумма входных сигналов превышает нулевое значение:

то выходной сигнал у = 1 и, следовательно, входное изображение Х^a принадлежит классу Х¹. Если S £ 0, то у = -1 и предъявленное изображение принадлежит второму классу.

Возможно использование отдельного нейрона и для выделения у множества классов

M = {X¹ = {X¹¹, ..., X^1k}, ..., Xⁱ = {Xⁱ¹, ..., X^iq}, ..., X^p = {X^p1, ..., X^pm}}

изображений единственного класса Xⁱ. В этом случае полагают, что один из двух возможных выходных сигналов нейрона (например, 1) соответствует классу Xⁱ, а второй - всем остальным классам. Поэтому, если входное изображение Х^a приводит к появлению сигнала у = 1, то X^a Î Xⁱ, если у = -1 (или у = 0, если используется бинарное кодирование), то это означает, что предъявленное изображение не принадлежит выделяемому классу.

Для адаптации, настройки обучения весов связей нейрона может использоваться несколько методов. Рассмотрим один из них, получивший название правила Хебба. В соответствии с правилом Хебба, если предъявленному биполярному изображению X = (x₁, .., x_n) соответствует неправильный выходной сигнал у , то веса 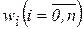связей нейрона адаптируется по формуле w_i(t+1) = w_i(t) + x_iy, 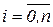, где w_i(t), w_i(t+1) - соответственно вес i-й связи нейрона до и после адаптации; 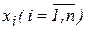- компоненты входного изображения; x₀ º 1 - сигнал смещения; у - выходной сигнал нейрона.

В более полной форме алгоритм настройки весов связей нейрона с использованием правила Хебба выглядит следующим образом:

Шаг 1. Задается множество M = {(X¹, U¹_вых), ..., (X^m, U^m_вых)}, состоящее из пар (входное изображение X^k = (x^k₁, ..., x^k_n), необходимый выходной сигнал нейрона U^k_вых), .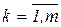

Инициируется веса связей нейрона: .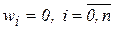

Шаг 2. Для каждой пары (Xx^k, U^k_вых), 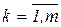, пока не соблюдается условия останова выполняются шаги 3-5.

Шаг 3. Инициируется множество входов нейрона: x₀ = 1, x_i = x_i^k,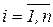

Шаг 4. Инициируется выходной сигнал нейрона: y = U^k_вых

Шаг 5. Корректируется веса связей нейрона по правилу: w_i(new) = w_i(old) + x_iy,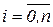

Шаг 6. Проверка условий останова.

Для каждого входного изображения X^k рассчитывается соответствующий ему выходной сигнал y^k:

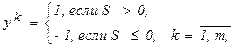где .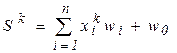

Если вектор (y¹, ..., y^m) рассчитанных выходных сигналов равен вектору (U¹_вых,..., U¹ⁿ_вых ) заданных сигналов нейрона, т.е. каждому входному изображению соответствует заданный выходной сигнал, то вычисление прекращается(выполняется шаг 7 ), если же (y¹, ..., y^m) ¹ (U¹_вых,..., U^m_вых ), то переход к шагу 2 алгоритма.

Шаг 7.Останов.

Использование группы из m биполярных нейронов A₁, ..., A_m (рис2) позволяет существенно расширить возможности сети и распознавать до 2^m различных изображений. Правда, применение этой сети для распознавания 2^m (или близких к 2^m чисел) различных изображений может приводить к неразрешимым проблемам адаптации весов связей нейросети.

Часто рекомендуют использовать данную архитектуру для распознавания только m различных изображений, задавая каждому из них единичный выход только на выходе одного А-элемента (выходы остальных нейронов при этом должны принимать значение -1).

Шаг 1. Задается множество M = {(X¹, U¹_вых), ..., (X^p, U^p_вых)} состоящее из пар (входное изображение X^k = (x^k₁, ..., x^k_n), необходимый вектор выходных сигналов нейронов U^k_вых = (U^k_вых1,..., U^k_{вых n} )),

Инициируется веса связей нейронов: .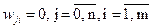

Шаг 2. Каждую пару (X^k, U^k_вых) проверяют на правильность реакции нейронной сети на входное изображение. Если полученный выходной вектор сети (y^k₁, ..., y^k_m) отличается от заданного (U^k_вых1,..., U^k_{вых m} ), то выполняются шаги 3 - 5.

Шаг 3. Инициируется множество входов нейронов: .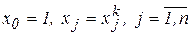

Шаг 4. Инициируются выходные сигналы нейронов: .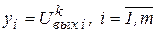

Шаг 5. Корректируют веса связей нейронов по правилу:

.

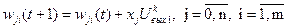Шаг 6. Проверяют условия останова, т. е. Правильность функционирования сети при предъявлении каждого входного изображения. Если условия выполняются, то переход к шагу 2 алгоритма, иначе - прекращение вычислений ( шаг 7).

Шаг 7. Останов.