Формирование множества критериев

Каждая альтернатива приводит к определенному исходу, последствия которого оцениваются по критериям, . Критериями будем называть такие показатели, которые:

1. признаются ЛПР в качестве характеристик степени достижения подцелей поставленной цели;

2. являются общими и измеримыми для всех альтернатив;

3. характеризуют общую ценность решения таким образом, что у ЛПР имеется стремление получить по ним наиболее предпочтительные оценки (т.е. они не могут быть представлены в виде ограничений).

При формировании множества критериев руководствуются двумя принципами:

1. принципом полноты

2. принципом простоты

Считается, что набор критериев является полным, если использование любых дополнительных критериев не изменяет результатов решения задачи, а отбрасывание хотя бы одного из выбранных критериев, наоборот, приводит к изменению результатов. Принцип простоты выражается в требованиях не избыточности (различные критерии из множества не должны учитывать один и тот же аспект последствий) и минимальности (множество должно содержать как можно меньше критериев).

Множество критериев является аппроксимацией рассматриваемой проблемы с точки зрения ЛПР, и формирование его является более искусством, чем наукой.

Шкалы

Сравнение альтернатив удается провести лишь в том случае, если интенсивности свойств, определяемых выбранными критериями, могут быть измерены у всех альтернатив. Таким образом, возникает необходимость в разработке оценочных шкал критериев. Типы шкал и основные их характеристики приводятся в табл. 3.

Таблица 3. Типы шкал и их основные характеристики

Тип шкалы	Аксиомы	Примечания. Примеры.
Номинальная (классифика- ционная)	Аксиома тождества:   · либо a~b, либо a ! ~ b · если a~b, то b~a · если a ~b и b~ c, то a~c	Отличительная черта : отсутствие математических свойств. Это крайний случай шкалы и она слабо используется для критериев.   Примеры: семейное положение (одинокий, женатый, разведён, вдовец); политическая принадлежность, группа крови и т. д.
Порядковая (ранговая)	Если, кроме вышеуказанных аксиом, удовлетворяет следующим аксиомам упорядоченности: · если a>b, то b · если a>b и b>c, то a>c	Отношение порядка не определяет расстояние между значениями шкалы.   Примеры : служебное положение, образование, воинское звание; шкалы силы ветра, твёрдости, землетрясения и т. п.
Интервальная	Если кроме указанных аксиом, можно ввести между любыми двумя значениями метрическое расстояние, т. е. какую-либо функцию, удовлетворяющую аксиомам : Эти шкалы могут иметь произвольные начала отсчёта и единицы длины, а связь между показаниями в таких шкалах является линейной :	Если два интервала в одной шкале , а при другом выборе начала отсчёта и единицы длины числами , то имеем   Примеры : температура (по Цельсию либо по Фаренгейту); время (у христиан – от рождества Христова, у мусульман - Магомета) и т. п.
Отношений	Если кроме вышеуказанных аксиом, выполняются аксиомы аддитивности : если a = p и b > 0, то a + b > p a + b = b + a; если a = p и b = g , то a + b = p + g ; (a + b) + c = a + (b + c)	Отношение двух значений шкалы не зависят от того, в какой из таких шкал произведены измерения Примеры : длина, вес, электрическое сопротивление, деньги.

Оценка альтернатив по шкалам критериев может быть проведена либо посредством физических измерений, либо экспериментальным путём. Под физическими измерениями понимаются не только собственно измерения технических или физических параметров, но и определение материальных, технико-экономических и т. п. показателей, которые могут быть вычислены существующими расчётными методами. Экспертные методы применяются в тех случаях, когда оценка альтернатив не может быть проведена на основе физических измерений [5].

Множество может содержать шкалы разных типов. Декартово произведение образует множество векторных оценок. Каждая альтернатива оценивается по шкалам , т. е. каждой альтернативе 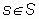ставится в соответствие n – мерная векторная оценка , где Xi – векторное значение i – го критерия по шкале Xi. Таким образом, множеству S ставится в соответствие множество векторных оценок 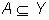с помощью отображения .

Основные элементы многокритериальной задачи принятия решения. понятие о Парето-множестве. Система предпочтений ЛПР. Решающее правило. Общая схема решения многокритериальных задач ПР.