Нейронные сети прямого распространения с непрерывной функцией активации: архитектура, алгоритмы обучения, применение.

Представленная на рис. конфигурация сигмоидальной нейронной сети функционирует следующим образом:

(1)

Цель обучения – настройка параметров (весов) сети таким образом, чтобы она реализовывала заданное соответствие между входным и выходным векторами. Для обучения выбирается множество 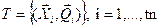, состоящее из соответствующих друг другу пар входных 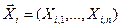и выходных 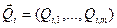векторов, на основании такого множества выполняется настройка параметров нейронной сети.

Качество обучения определяется средней ошибкой нейронной сети на всем обучающем множестве

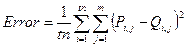. (2)

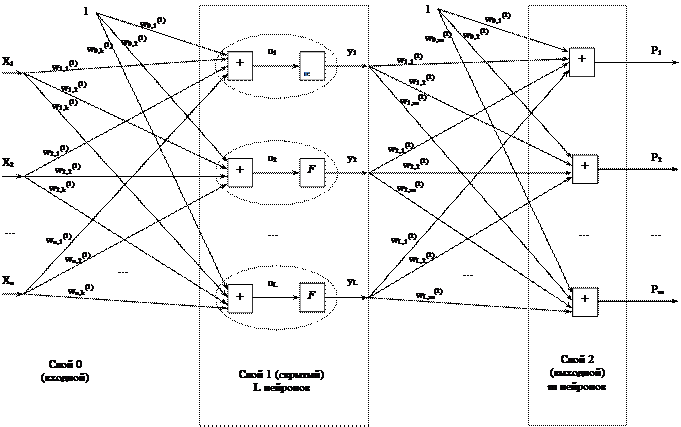
Рис. 1. Двухслойная сигмоидальная нейронная сеть.

Алгоритм обучения разработан на основе метода обратного распространения ошибки. Он содержит модификации, включающие пакетное обучение (обучение по эпохам) и применение импульса весов связей сети, и состоит в следующем:

1. Веса связей скрытого и выходного слоев 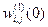и и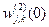нициализируются случайным образом. Приращения весов связе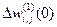й и 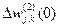инициализируются нулевыми значениями. Выбирается значение коэффициента обучения α из диапазона [0.001; 1] и значение коэффициента импульса (определяющего вклад в приращение весов сети результатов предыдущих итераций) β из диапазона [0.1; 0.9]. Задается точность обучения ε.

2. Суммы градиентов весов связей и 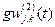инициализируются нулевыми значениями.

Для каждой пары векторов 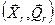из обучающего множества выполняются шаги 2.1-2.2.

2.1. Вектор 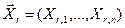подается на вход нейронной сети и вычисляются выходы нейронной сети

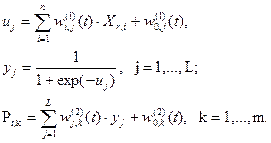(3)

2.2. К сумме градиентов весов добавляются частные производные функции ошибки, вычисленные для обучающей пары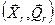

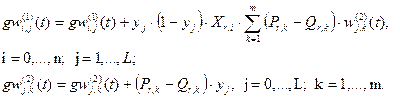(4)

При этом принимается .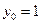

3. Вычисляются новые приращения весов на основе суммы градиентов и предыдущих приращений

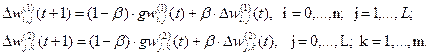(5)

4. Корректируются веса связей

(6)

5. Если средняя ошибка нейронной сети (2) достигла приемлемого значения 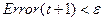, то вычисления завершаются, иначе выполняется переход к п.2.

В приведенном выше алгоритме t=0,1,… означает номер шага вычислений (эпохи), который соответствует количеству предъявлений обучающего множества для настройки сети. Соответственно, 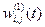, например, означает значение веса 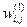на t-ом шаге вычислений.

8. Сравнительный анализ парадигм исследования операций и принятия решений. Классификация типов проблем по Г. Саймону.

Парадигма – признанное всеми научное достижение, которое в течение определённого времени дает научному сообществу модель постановки проблем и их решение. Под исследованием операций (ИО) понимают применение математических количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.

Сравнительный анализ парадигм.

Особенности парадигмы ИО:

1. Объектный характер использования моделей, т. е. опираясь на одни и те же данные, различные специалисты-аналитики должны получать одинаковые результаты. Построение моделей рассматривается как средство отображения объективно существующей реальности.

2. Задачи ИО рассматриваются по заказу руководителей. Получив такой заказ, аналитик исследует проблему и пытается найти адекватную модель. В этой работе сам руководитель не нужен, т. е. он делает заказ и получает готовые решения.

3. Существует объективные критерии успехов применения методов ИО. С ним нельзя спорить.

Особенности парадигмы ПР:

1. Модель зависит от личности ЛПР (системы ценностей). Эта субъективность является единственно возможной основой объединения критериев проблемы в единую модель, позволяющую оценивать варианты решений.

2. Аналитик помогает принять решение руководителю. Эта помощь заключается в том, что он изучает объективные параметры модели. А также проводит исследование по выявлению предпочтений ЛПР, изучение его системы ценностей.

3. Выбирается лучший вариант, исходя из системы предпочтений конкретного ЛПР. Признание ответственности ЛПР за принятые решения позволяет резко усилить их мотивацию к тщательному анализу варианта.

Существуют большие различия в природе изучаемых проблем. Саймон предложил следующую классификацию проблем:

· Хорошо структурированные – количественно сформулированные проблемы, в которых существенные зависимости выяснены хорошо и могут быть выражены в числах или символах, получающие в конце концов численные оценки задачи ИО.

· Неструктурированные или качественно выраженные проблемы, т.е. количественной зависимости между элементами этой проблемы совершенно не известны.

· Слабо структурированные или смешанные проблемы содержат качественные и количественные элементы. Причем качественные мало известные и неопределенные стороны проблем имеют тенденцию доминировать.

Согласно этой классификации типичные проблемы ИО можно назвать хорошо структурированными.