Анализ алгоритмов линейного поиска

Для отыскания искомого элемента с использованием алгоритмов линейного поиска в худшем случае придется просмотреть все N элементов массива, следовательно порядок функции ВС будет O(N). В лучшем случае, когда искомый элемент равен первому элементу массива, число сравнений не зависит от количества элементов в массиве и порядок функции ВС будет O(N).

Оценим среднее время алгоритма, при этом будем исходить из следующего:

пусть P_i – вероятность того, что будет осуществляться поиск элемента со значением k_i; предположим, что 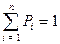, т.е. элемент со значением k_i не будет отсутствовать (в массиве обязательно есть элемент, поиск которого осуществляется).

Среднее время ( 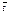), как следует из алгоритма, пропорционально среднему числу операций сравнения ( 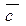) и равно 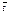~ = 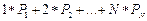. Если ключи имеют одинаковую вероятность P₁=P₂=...P_N=P, а также учитывая, что , N*P=1, P=1/N, тогда ,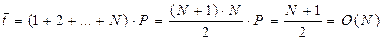

т.е. при линейном поиске в среднем необходимо просмотреть половину массива.

Для экспериментального определения среднего числа сравнений необходимо найти суммарное число сравнений при поиске всех элементов массива и разделить на количество элементов.