
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы принятия решений на основе аналитико-сетевого процесса.
Аксиома №1 связана с обратными значениями.
Аксиома №2 связана с гомогенностью.
Аксиома №3 связана с иерархической композицией.
Последняя аксиома требует тщательной экспертизы в отличие от первых двух. В задаче выбора предпочтительных альтернатив всегда зависит от элементов более высшего уровня, в то время как важность целей может зависеть от элементов нижнего уровня. Если это имеет место, то третья аксиома не применима, то есть в этом случае имеет место проблема, структура которой имеет обратную связь, что может быть описано в виде орграфа (сети):

Обычно один из кластеров объединяет альтернативы.
Этап I: принцип идентичности и декомпозиции. На начальном этапе исследования должна быть чётко сформулирована цель, в терминах которой будут определяться основные подходы к категориям (кластеры, элементы, суждения). Элементы задачи принятия решения, критерии, атрибуты объединяются в кластеры, между которыми возможны произвольные связи. Кластер имеет внешнюю зависимость, когда его элементы или хотя бы один связан с элементами, которые тоже могут быть кластерами. Кластер может иметь внутреннюю зависимость (E), когда его элементы связаны с другими элементами в том же классе, например, в E. Таким образом, кластеры в АСП обычно не являются простой совокупностью элементов. Они представляют обычную систему и тем самым отличаются от элементов (Эмердженстность (целостность): свойства системы не являются простой суммой свойств составляющих её элементов). Формирование кластеров и связей – неформальная процедура и осуществляется ЛПР и экспертом на основе конкретных знаний и специфики решения задачи. Итог – граф, вершинами которого являются кластеры, а дуги отражают влияние кластеров друг на друга.
 ,
, 
 ;
;  ;
; 
 ;
; 

Здесь N – количество кластеров; ki – количество элементов в i-ом кластере; M – общее количество элементов; .
.
Этап II: реализуется принцип дискриминации сравнительных сужденийи заключается в построении МПС сначала для кластеров, а затем для элементов. Иерархии, используемые в АИП, связаны с распространением качества (целей) среди сравниваемых элементов, то есть, чтобы определить у какого из них количество данного качества преобладает. Сети связаны с распределением влияния элементов на некоторые другие элементы относительно данного качества (цели), то есть влияние – ключевое качество. Степень влияния кластеров друг на друга сводится к формированию матрицы NxN:
| ij | … | N | ||||
| ||||||
| … | ||||||
| N |
Заполнение происходит по столбцам. В j-ом – веса влияния j-го кластера, полученного в результате обработки МПС на все остальные кластеры в соответствии с графом. Если кластер не влияет на какой-нибудь другой, то в матрице там ставится 0, если же влияет только на один кластер, то записывается 1.
Для каждого столбца рассматриваемой матрицы может быть построена МПС, при заполнении которой эксперт отвечал на вопросы: на какой из сравниваемых кластеров в указанных строках рассматриваемый кластер, обозначающий процесс, оказывает большее влияние и на сколько большее относительно цели.

Следующий шаг: формирование матриц парных сравнений уже для элементов кластеров и вычисление их приоритетов, на основании которых формируется супер матрица размерностью MxM.
| j | N | |||||
| W11 | W12 | … |
| |||
| W21 | W22 | … | W2N | |||
| i | … | … | Wij | … | ||
| N | WN1 | WN2 | … | WNN |
| ij | j.1 | j.2 | … |
| ||
| i.1 | ||||||
| i.2 | ||||||
| … | ||||||
| i.ki |
Рассмотрим блок заполнения матрицы Wij размерностью KiKj. Заполнение – по столбцам.
1. Если j-ый кластер не влияет на i-ый, то блок размерностью kixkj заполняется нулями.
2. Если влияет, то может быть два варианта: элемент j.kj не влияет на i.ki, тогда столбец j.kj заполняется 0; если же влияет, то в данный столбец записываются веса влияния, полученные в результате обработки МПС на элементы i.ki.
После формирования получают взвешенную матрицу W* путём умножения каждой блочной матрицы Wij на Vij, полученной при рассмотрении задачи влияния кластеров. Такая нормировка суперматрицы даёт свойство: сумма значений каждого столбца W* равна 1.
Этап III: синтез. Нас интересуют приоритеты двух типов, которые показывают влияние одного элемента на любой другой и известны, как относительные приоритеты; другие приоритеты – абсолютные приоритеты любого элемента безотносительно того на какие элементы он влияет. Третий этап определяет абсолютные приоритеты, которые соответствуют устойчивому предельному состоянию системы с обратными связями. Определение такого устойчивого состояния основывается на теореме: если W* - примитивная и стохастическая по столбцам, то имеет место:  ; k = 1, 2, ... Здесь w – матрица, имеющая одинаковые столбцы, единственный вектор равновесной вероятности, элементы которого не меняются при дальнейшем увеличении изменения степени. Если матрица имеет единственный собственный вектор, то данная матрица – примитивная.
; k = 1, 2, ... Здесь w – матрица, имеющая одинаковые столбцы, единственный вектор равновесной вероятности, элементы которого не меняются при дальнейшем увеличении изменения степени. Если матрица имеет единственный собственный вектор, то данная матрица – примитивная.
Неотрицательная матрица W* - стохастическая тогда и только тогда, когда решением уравнения e*W* = e, где e = (1,1, ..., 1) является единственный вектор. Максимальное собственное число lmax = 1.
Столбец из матрицы w и связывается с абсолютными предельными приоритетами, которые можно интерпретировать как прогнозируемые значения вклада рассматриваемых факторов в цель с учётом их взаимного влияния. Показатель, который может иметь высокое значение – большее значение, так как накапливает в себе влияние других факторов.
Основные идеи в поддержку АСП:
1. Не постулируются предположения о независимости элементов высоких уровней от элементов более низких уровней и независимость элементов в пределах уровня. Следовательно, АИП рассматривается как частный случай АСП.
| N | |||||
| W21 | |||||
| W31 | |||||
| N | WN,N-1 |
2. АСП располагает по приоритетам не только элементы, но так же и кластеры элементов.
3. АСП не линейная структура, которая имеет дело с истоками, циклами и стоками. Иерархия же линейная с целью на верхнем уровне и альтернативами на нижнем уровне. Это тоже различие.
4. АСП, можно сказать, более свободная структура, делает возможным представление любой проблемы без учёта (как это требует АИП): что необходимо выполнить сначала, а что после.
Рассмотренный подход прогнозирования имеет ряд преимуществ. Важнейшие из них:
-возможность построения модели на основе экспертной информации, в том числе учёт влияния качественных факторов (в отличие от различных статистических подходов);
-возможность проверки различных гипотез в структуре интенсивности влияния различных факторов.
15. Применение нечетких множеств в СППР. Обоснование подхода. Принцип несовместимости. Элементы теории нечетких множеств.
Согласно глубоко укоренившейся традиции научного мышления, начиная с Декарта, понимание какого-либо процесса или явления отождествляется с возможностью его количественного анализа. В настоящее время, однако, правомерность такого анализа, основанного на использовании дифференциальных или конечно-разностных уравнений для описания систем, в которых участвует человек (слабоструктурированных и неструктурированных), подвергается сомнению.
Системы, неотъемлемым (или даже основным) фактором которых является именно человек и его суждения, относятся к классу так называемых слабоструктурированных систем (СС-систем), для которых обычные количественные методы анализа и описания не применимы по своей сути. В основе этого тезиса лежит принцип несовместимости, сформулированный Заде, который утверждает, что чем сложнее система, тем менее мы способны дать точные и в то же время имеющие практическое значение суждения. Для систем, сложность которых превосходит некоторый пороговый уровень, точность и практический смысл, т.е. содержательность, становятся почти взаимоисключающими характеристиками.
Именно в этом случае точный количественный анализ СС-систем не имеет большого практического значения при решении реальных экономических, социальных, политических и других задач, сравнимых по сложности и связанных с участием одного человека или гоуппы людей. В данных случаях действует принцип: "Точность - это ложь".
Альтернативный подход состоит в том, что ключевыми элементами мышления являются не числа, а понятия, которые по своей сути являются нечёткими в силу индуктивности мышления человека.
Индукция - способ обнаружения закона для бесконечного числа данных по конечному числу данных. Однако подобное принципиально невозможно, следовательно, результат индуктивных выводов всегда нечёток, а логика размышления человека не является двузначной, а многозначной и даже может быть непрерывной.
Таким образом для радикального изменения работы слабоструктурированных и неструктурированных систем необходимы подходы, которые не фетишизируют такие понытия как точность, строгость, математический формализм, а используют методологические схемы, содержащие нечёткость и неполную истинность.
Язык нечётких множеств и алгоритмов в настоящее время наиболее адекватный математический аппарат, который позволяет максимально сократить переход от вербального словестного качественного описания объекта, которое характеризует человеческое мышление, к численным количественным оценкам его состояния и сформулировать на этой основе простые и эффективные алгоритмы, то есть позволяет моделировать человеческие размышления и человеческую способность решения задач.
Основные понятия и определения.Множество – (основоположник Хантор). Множество – многое мыслимое как единое.
Задавать множества можно перечислением {ai}, где  или путём указания некоторого свойства, например множество студентов, множество A и так далее.
или путём указания некоторого свойства, например множество студентов, множество A и так далее.
Пусть X – это множество, а A – подмножество X, тогда xi Î A. Характеристическая функция  .
.
Пример:
X = {1, 2, 3, 4, 5, 6}
A = {2, 4, 5}
mA(2) = 1, mA(4) = 1, mA(5) = 1, а остальные = 0.
A = {0/1; 1/2; 0/3; 1/4; 1/5; 0/6}
Однако, как показала практика исследования подобный булевый принцип (Ï или Î) в подавляющем большинстве случаев не отвечает процессам, то есть приводит к неопределённой детализации математических процессов системы.
Нечётким множеством A| на множестве X называется совокупность пар A| = {mA|(x)/x}, где mA|: x ® [0, 1] – функция принадлежности; mA(x) – степень принадлежности x нечёткому множеству A|.
X· – базовое множество той или иной предметной области.
Если X· – непрерывное множество, то  , ò - знак объединения.
, ò - знак объединения.
Если X· – дискретное множество, то 
Интерпретации степени принадлежности являются согласно Заде субъективной мерой того, на сколько элемент x Î X, соответствует понятию, смысл которого формализация с нечётким множеством A|.
Носитель A|: Supprt (A|) = {x|x Î X Ù mA|(x) > 0};
Ядро A|: Core (A|) = {x|x Î X Ù mA|(x) = 1}.
 “разумное количество детей в семье” = {0.1/0; 0.3/1; 0.7/2; 1/3; 0.7/4; 0.3/5; 0.1/6}.
“разумное количество детей в семье” = {0.1/0; 0.3/1; 0.7/2; 1/3; 0.7/4; 0.3/5; 0.1/6}.
 “скорость около 50 км/ч”.
“скорость около 50 км/ч”.
mA|(x) = 1/1 + ((50 – x)/10)h;

 “хорошая машина” = {0.3/Волга; 0.7/Москвич; 1/Жигули; 0.1/Ока}. Здесь X = {“Волга”, “Москвич”, “Ока”, “Жигули”}.
“хорошая машина” = {0.3/Волга; 0.7/Москвич; 1/Жигули; 0.1/Ока}. Здесь X = {“Волга”, “Москвич”, “Ока”, “Жигули”}.
Sup mA|(x) = 1 (x Î X) – если это не выполняется, то множество субнормальное.
A| Ì B| Û mA|(x) < mB|(x), " x Î X$
A| = B| Û mA|(x) = mB|(x);
Интерпретацией значений mA|(x) может являться вероятность того, что ЛПР отнесёт элемент x ко множеству A|.
Если A| - нечёткое понятие, то mA|(x) – вероятность того, что ЛПР использует A| в качестве имени объекта.
Алгебра нечётких множеств.Как и в обычной теории множеств, для нечётких множеств вводятся операции объединения, пересечения, дополнения.
Объединением A| и B| на множестве X (нечёткая дизъюнкция) называют  ;
;  .
.

Пересечением A| и B| на множестве X (нечёткая конъюнкция) называют  ;
;  .
.

Дополнение (отрицание): 
Условия:
1. алгебра чётких множеств – частный случай операции;
2. функции принадлежности операции пересечения должны быть не больше, а функция принадлежности объединения не меньше, чем функция принадлежности каждому из множеств A| и B|.
3. Должны быть законы:
· A| Ç B| = B| Ç A|;
· A| È B| = B| È A|;
· Ассоциативность: A| Ç (B| Ç C|) = (A| Ç B|) Ç C|;
· Дистрибутивность:
A| Ç (B| È C|) = (A| Ç B|) È (A| Ç C|);
A| È (B| Ç C|) = (A| È B|) Ç (A| È C|);
· ù (ùA|) = A|;
· ù (A| Ç B|) = ùA| È ùB|;
· ù (A| È B|) = ùA| Ç ùB|;
Не выполняются законы:
· ù A Ç B = 0;
· ù A| Ç B| É 0;

Если интерпретация функции принадлежности вероятностная, то операции пересечения и объединения задаются по-другому.
 ;
;
 .
.
Операция декартового произведения:
Пусть:
A|1 » X1
A|2 » X2, тогда  ;
;
Пример:
X1 = X2 = 3 + 5 + 7;
A|1 = 0.5/3 + 1/5 + 0.6/7;
A|2 = 1/3 + 0.6/5 + 0/7;
A|1 x A|2 = 0.5/3.3 + 0.5/3.5 + ...
| 0,5 | 0,6 | ||
| 0,5 | 0,6 | 0,6 | |
Возведение в степень:  ;
;
e = 2 CON (A|) = A|2;
e = 0.5 DIL (A|) = A|0.5.
Расстояние между нечёткими множествами
Если A| и B| - нечёткие множества, то расстояние между ними определяется аксиомами:
(A|,B|) > 0;
p(A|,A|) = 0;
p(A|,B|) = p(B|,A|);
p(A|,B|) £ p(A|,C|) + p(C|,B|);
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Индексы нечёткости.При оценке нечёткости используется два подхода:
1. метрический: двусмысленность объекта x в отношении A, который проявляется в следующем – с одной стороны он принадлежит классу объектов, обладающих свойством A, с другой стороны принадлежит классу объектов, не обладающих свойством A.
 -
-  ; min, когда
; min, когда  или 0.
или 0.
Введём функционал d(A|):
· d(A) = 0;
· d(A|) " x ;
· B| d(B|) > d(A|);
· d(A|) = d(ùA|).

Ближайшее чёткое множество к A|, согласно Евклидову расстоянию, определяется с помощью характеристической функции:

Линейный индекс нечёткости:  .
.
Квадратичный индекс нечёткости:  .
.
2. энтропийный:  ;
;  ;
;  ;
;
 0 £ m £ 1
0 £ m £ 1
Нормировка:
 ;
;  ;
;
 ;
; 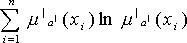 .
.
H максимальна, когда все элементы имеют одинаковую степень принадлежности, и минимальна, когда A| - одноточечное множество. То есть зависит не от абсолютных значений, а от относительных.
Дата добавления: 2015-04-18; просмотров: 311; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 ;
; 