
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип дискриминации и сравнительных суждений.
Данный принцип реализуется на втором этапе МАИ. Суть его заключается в том, что, используя суждения ЛПР/эксперта и определенные алгоритмы их обработки, устанавливаются веса 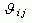 дуг (i,j)
дуг (i,j) 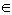 W и веса
W и веса 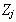 объектов первого уровня(
объектов первого уровня(  ). Если на первом уровне один объект, то вес его принимается за 1 (
). Если на первом уровне один объект, то вес его принимается за 1 (  = 1).
= 1).
Суждения ЛПР/эксперта являются результатом исследования его структуры предпочтений. При этом исследовании применяется метод парных сравнений, содержание которого состоит в следующем. Пусть задано некоторое фиксированное множество объектов  , которые сравниваются попарно с точки зрения их предпочтительности, желательности, важности и т. п. Результаты записываются в виде матрицы парных сравнений
, которые сравниваются попарно с точки зрения их предпочтительности, желательности, важности и т. п. Результаты записываются в виде матрицы парных сравнений  .
.
Результат сравнения отражает не только факт, но и степень (силу, интенсивность и т.п) превосходства. При этом используется шкала относительной важности, выбор которой зависит от следующих требований:
· шкала должна давать возможность улавливать различия в ощущениях людей, когда они проводят сравнение;
· диапазон измеряемой интенсивности шкалы должен соответствовать результатам когнитивной психологии.
Шкала относительной важности.
| Количественная оценка интенсивности относительной важности | Качественная оценка интенсивности относительной важности | Комментарий |
| Равная важность | Равный вклад двух объектов | |
| Умеренное превосходство одного над другим | Опыт и суждения дают легкое превосходство одного объекта над другим | |
| Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одного объекта над другим | |
| Значительное превосходство | Один объект имеет настолько сильное превосходство, что оно становится практически значительным | |
| Очень сильное превосходство | Очевидность превосходства одного объекта над другим подтверждается наиболее сильно | |
| 2,4,6,8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссном случае |
| Обратные величины приведенных выше чисел (1/2,1/3,1/4,…,1/9) | Если объекту i при сравнении с объектом j приписывается одно из приведенных выше чисел, то действию j при сравнении с i приписывается обратное значение |
Обоснование процедуры перевода полученных значений стимула в ощущение.
 - не будет изменяться, если
- не будет изменяться, если 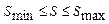 .
.
Закон Веббера-Фехнера гласит, что различия в ощущениях становятся заметными, когда значение стимула увеличивается на некоторый постоянный процент от начального значения. В 1860г Веббер сформулировал последовательность предельно значимых различий в стимулах.
S0 – первое значение стимула.

Таким образом, значимые различия в стимулах описываются геометрической прогрессией. Соответствующие стимулам ощущения описываются арифметической последовательностью дискретных точек. Эти точки можно получить, выразив n из последнего соотношения.

Если ощущения обозначить через M, а стимулы через S, то закон будет иметь следующий вид:
 , т.е. линейная функция от логарифма стимула.
, т.е. линейная функция от логарифма стимула.
Пусть S0=1, b=0

Разделив Mi на M1 мы получим последовательность чисел фундаментальной шкалы.
Из шкалы следует свойство гомогенности (однородности) объектов. Это свойство соответствует способности людей сравнивать объекты, которые не слишком сильно отличаются друг от друга. Гомогенность существенна для сравнения объектов одного порядка, т.к. человеческий разум склонен к допущению больших ошибок при сравнении несопоставимых элементов. Суждения вне порядка (>10) обычно приводят к снижению точности, к увеличению противоречивости (вторая аксиома Саати). Когда эта несопоставимость большая, объекты располагаются в отдельные кластеры сравниваемых размеров, что выдвигает идею об уровнях и их декомпозиции.
Пример: Допустим необходимо оценить предпочтения ЛПР/эксперта на множестве вариантов А, В, С относительно критерия - размера дома. Лучше всего эту задачу свести к заполнению таблицы:
| Размер дома | A | B | C |
| A | 1/3 | ||
| B | 1/7 | ||
| C | 1/5 |
Размерность таблицы определяется количеством дуг, которые входят в рассматриваемую вершину. Элементы таблицы 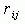 , i, j = 1, 3 являются количественной оценкой интенсивности предпочтения i - го объекта, находящегося в i - й строке, относительно j - гo объекта, находящегося в j - м столбце, в соответствии с вышерассмотренной шкалой. При этом сравнении ЛПР/эксперту задаётся два вопроса: какой из двух объектов предпочтительнее и в какой степени один объект предпочтительнее другого? Ответом ЛПР/эксперта, как следует из таблицы, было следующее суждение: существенное или сильное превосходство.
, i, j = 1, 3 являются количественной оценкой интенсивности предпочтения i - го объекта, находящегося в i - й строке, относительно j - гo объекта, находящегося в j - м столбце, в соответствии с вышерассмотренной шкалой. При этом сравнении ЛПР/эксперту задаётся два вопроса: какой из двух объектов предпочтительнее и в какой степени один объект предпочтительнее другого? Ответом ЛПР/эксперта, как следует из таблицы, было следующее суждение: существенное или сильное превосходство.
Таким же образом осуществляется оценка предпочтений ЛПР/эксперта относительно остальных критериев путем заполнения еще пяти аналогичных матриц размерностью 3x3. После чего метод парных сравнений распространяется на множество самих критериев относительно Цели - покупки дома. В этом случае ЛПР/эксперту задается следующий вопрос: насколько важнее один критерий (например, размер дома) для Реализации цели по сравнению с другим (например, финансовые условия)? Как следует из иерархии, размерность этой таблицы 6x6.
Принимая во внимание свойство матрицы, т. е.  и, как следствие,
и, как следствие,  =1, количество вопросов равно n*(n-1)/2
=1, количество вопросов равно n*(n-1)/2
Формализацией понятия непротиворечивости для метода парных сравнений является выполнение следующего равенства:
 (1)
(1)
где  - это элементы матрицы полученные в результате идеально согласованного эксперимента. Соотношение (1) соответствует правилу логического вывода, которое в этом случае формулируется следующим образом: если i-й объект предпочтительнее k-го объекта на
- это элементы матрицы полученные в результате идеально согласованного эксперимента. Соотношение (1) соответствует правилу логического вывода, которое в этом случае формулируется следующим образом: если i-й объект предпочтительнее k-го объекта на  и k-й объект предпочтительнее j-го объекта на
и k-й объект предпочтительнее j-го объекта на  , то i-й объект предпочтительней j-го объекта на
, то i-й объект предпочтительней j-го объекта на  , причем
, причем  .
.
Теорема. Если матрица  обладает свойством (1), то тогда существуют такие числа
обладает свойством (1), то тогда существуют такие числа  , что имеет место равенство
, что имеет место равенство
 (2)
(2)
Числа  отождествляются с весами дуг (это множество W в графе G) либо с весами объектов первого уровня (это
отождествляются с весами дуг (это множество W в графе G) либо с весами объектов первого уровня (это  ).
).
Матрица  имеет единичный ранг,
имеет единичный ранг,  ,
,  собственный вектор матрицы, где n - соответствующее ей собственное число.
собственный вектор матрицы, где n - соответствующее ей собственное число.
Действительно,
 (3)
(3)
Практически добиться полной согласованности (т.е. непротиворечивости) суждений ЛПР/эксперта далеко не всегда возможно. Поэтому в общем случае  будут отклоняться от "идеальных"
будут отклоняться от "идеальных"  , вследствие чего соотношения 1, 2, 3 не будут иметь место.
, вследствие чего соотношения 1, 2, 3 не будут иметь место.
Для дальнейшего анализа полезными являются следующие два факта из теории матриц:
· Во-первых, если  являются собственными числами матрицы R и если
являются собственными числами матрицы R и если  . Согласно этому утверждению, если имеет место (3) (т.е. матрица является идеально согласованной), то все собственные числа ее - нули, за исключением одного, равного n.
. Согласно этому утверждению, если имеет место (3) (т.е. матрица является идеально согласованной), то все собственные числа ее - нули, за исключением одного, равного n.
· Во-вторых, если элемент положительной обратносимметричной матрицы R незначительно изменить, то собственные числа этой матрицы также изменятся незначительно, т.е. они являются непрерывными функциями ее элементов.
Объединяя эти результаты, находим, что при малых изменениях  от
от  наибольшее собственное число
наибольшее собственное число  (практически получаемой матрицы R при использовании метода парных сравнений) остается близким к n, a остальные собственные значения - близкими к нулю.
(практически получаемой матрицы R при использовании метода парных сравнений) остается близким к n, a остальные собственные значения - близкими к нулю.
Отсюда можно сформулировать следующую задачу: для нахождения весов дуг или объектов первого уровня по полученной в результате метода парных сравнений матрице R необходимо определить собственный вектор  , соответствующий максимальному собственному числу, т.е. решить уравнение:
, соответствующий максимальному собственному числу, т.е. решить уравнение:
 (4)
(4)
Так как малые изменения в  ,
,  вызывают малое изменение
вызывают малое изменение  , отклонение последнего от n является мерой согласованности. Она может быть выражена с помощью индекса согласованности (ИС):
, отклонение последнего от n является мерой согласованности. Она может быть выражена с помощью индекса согласованности (ИС):
 (5)
(5)
Если ИС<= 0,1, то практически считается, что мера согласованности находится на приемлемом уровне.
Индекс согласованности матрицы парных сравнений, элементы которой сгенерированы случайным образом, называется случайным индексом (СИ). Ниже представлена таблица соответствия порядка и среднего значения СИ, определенная на базе 100 случайных выборок:
| Порядок матрицы | ||||||||||
| СИ | 0,00 | 0,00 | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС). Значение ОС меньшее или равное 0,10 считается приемлемым. Обычно ИС и ОС указываются в процентах. Согласно определению, ИС можно трактовать как отклонение от идеально проведенного эксперимента (метода парных сравнений), а ОС указывает, на сколько оцениваемая степень согласованности сходится со степенью согласованности самого неидеально проведенного эксперимента.
Таким образом, МАИ допускает несогласованность (как неотъемлемую часть метода), признавая, что человеческие суждения находятся в постоянном процессе изменения и эволюции (поэтому не следует настаивать на 100 % согласованности, так как суждения могут измениться после того, как проблема решена). Но надежные решения не могут быть приняты без приемлемого уровня согласованности.
Существуют два метода решения уравнения  . Это прямой и итерационный.
. Это прямой и итерационный.
Рассмотрим прямой метод. Проверим алгоритм данного метода. R - идеально согласованная матрица, т. е.

1. Определим среднее геометрическое каждой строки R

2. Вычислим сумму средних геометрических полученных в п. 1

3. Разделим среднее геометрическое каждой строки R (п. 1) на значение, полученное в п. 2

т. е. получили нормированное значение собственного вектора. Для получения  выполним следующие шаги:
выполним следующие шаги:
4. Определим сумму элементов для каждого столбца матрицы R

5. Определим скалярное произведение векторов, полученных в п. 3 и в п. 4

что соответствует максимальному собственному числу для идеально согласованной матрицы. Итерационный метод основан на следующей теореме: для положительной квадратной матрицы R собственный вектор V, соответствующий максимальному собственному значению  , с точностью до постоянного сомножителя C определяется по формуле:
, с точностью до постоянного сомножителя C определяется по формуле:

где  - единичный вектор
- единичный вектор
k = 1, 2, 3,… показатель степени
C – константа
Т – знак транспонирования
Вычисление собственного вектора V производится до достижения заданной точности:

где l – номер итерации, такой, что l = 1 соответствует k = 1; l = 2, k = 2 и т. д.
 - допустимая погрешность
- допустимая погрешность
С достаточной для практики точностью принимается = 0,01 независимо от порядка матрицы.
Максимальное собственное значение вычисляется по формуле

В результате обработки матрицы получаем локальные приоритеты, которые представляют собой приоритеты элементов группы по отношению к родителю.
Дата добавления: 2015-04-18; просмотров: 355; Мы поможем в написании вашей работы!; Нарушение авторских прав |