
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Композиционное правило вывода.
Это правило является решающим в нечёткой среде и является обобщением известной процедуры на нечёткие множества:
Заданы следующие предпосылки:
1. y = f(x);
2. x = a.
y = f(a) = b - вывод
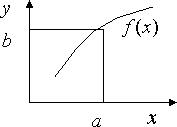
Распространим эту процедуру, когда функция является интервальной, аргументы тоже являются интервальными:
|

F(x,y) – данную функцию можно считать как нечёткое бинарное отношение на декартовом произведении 0X*0Y.
|

Пусть задано следующее:



Строим: 
Нужно определить:  , для чего выполняем следующее
, для чего выполняем следующее  - по определению, так как
- по определению, так как  - цилиндрическое множество.
- цилиндрическое множество.
 - композиционное правило вывода на языке выражений (функция принадлежности).
- композиционное правило вывода на языке выражений (функция принадлежности).
Запишем его теперь на языке множеств.
Пусть R|(x), R|(x,y), R|(y) – ограничения на переменные x, (x,y), y, которые являются нечёткими множествами на множествах X, XxY, Y.
Пусть A| и F| - нечёткие множества на X и XxY, тогда композиционное правило утверждает, что уравнения назначения: предпосылки Þ  ;
;  и решения их относительно Y имеет вид R(y) = A| ° F| - вывод.
и решения их относительно Y имеет вид R(y) = A| ° F| - вывод.
Пример, пусть X=1+2+3. Множество  и второе уравнение назначения:
и второе уравнение назначения:
| |||||
| 0.7 | 0.3 | ||||
| 0.7 | 0.7 | ||||
| 0.3 | 0.7 |
Тогда можем вычислить характеристики нечёткого отношения R|(y) = “малый” ° “приблизительно равны” =  .
.
Правило modus ponens как частный случай композиционного правила вывода. <A→B> - истина и <A> - истина, то <B> - истина. Это силогизм – дедуктивное умозаключение, в котором одно суждение является необходимым следствием двух других.
| B\A | + |
| ||
| + | + | - | ||
| - | + | + |
В обычных рассуждениях выражение “если A, то B” употребляется в ситуациях, когда A и B – нечёткие понятия. Например, если помидор – красный, то он – спелый. Чтобы обобщить понятия импликации на нечёткие подмножества, предположим, что X, Y – чёткие множества, на которых задаются нечёткие множества A|, B|, C|. Если A| то B| иначе C| 
Определение (по Заде). Высказывание “если A| то B| иначе C |” – это бинарное нечёткое отношение на XxY и определяется следующим образом:  .
.
Если A| то B| иначе C|  - частный случай при допущении, что C| - полное множество, то есть C| = Y.
- частный случай при допущении, что C| - полное множество, то есть C| = Y.
|

То, что после “если” – онтецедент, после “то” – консеквент. В сущности, последнее правило равнозначно “если A то B иначе безразлично”.
Рассмотрим пример:
X=Y = 1+2+3



Если A| то B| иначе C| = (1/1+0.4/2)x(0.4/2+1/3)È(0.6/2+1/3)x(1/1+
| |||||
| 0.4 | |||||
| 0.6 | 0.6 | 0.4 | |||
| 0.6 |
Если A| то B|  (1/1+0.4/2)x(0.4/2+1/3)È(0.6/2+1/3)x(1/1+1/2+1/3).
(1/1+0.4/2)x(0.4/2+1/3)È(0.6/2+1/3)x(1/1+1/2+1/3).
Рассмотрим связь между правилом modus ponens и композиционным правилом вывода и определим обобщённое правило modus ponens.
Определение. Пусть  - нечёткие подмножества множеств X, X, Y. Предположим, что
- нечёткие подмножества множеств X, X, Y. Предположим, что  назначена отношению R(x,y),
назначена отношению R(x,y),  , то получим следующие уравнения:
, то получим следующие уравнения:
 - правило
- правило
 - факт
- факт
 - обобщённое правило modus ponens
- обобщённое правило modus ponens
Эти уравнения назначения в композиционном правиле вывода в отношениях можно разрешить относительно ограничения на Y.
Приведённая формулировка отличается от классической:
1.  - нечёткие множества;
- нечёткие множества;
2.  не обязательно идентично
не обязательно идентично  ;
;
3. Если импликацию задавать по Заде  , то
, то  - если это чёткие множества.
- если это чёткие множества.
Пример:
X=Y = 1+2+3
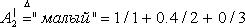


| |||||
| 0.4 | |||||
| 0.6 | 0.6 | 0.6 | |||
“средний” ° (“малый” → “большой”) = (0.6 0.6 0.6)
Дата добавления: 2015-04-18; просмотров: 317; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 - полное множество
- полное множество
 - цилиндрическое множество
- цилиндрическое множество

