
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многокритериальный выбор альтернатив на основе нечетких множеств.
Дано: {Sj};  ; {Ki};
; {Ki};  . Каждому критерию ставится в соответствие нечёткое множество. Базовое множество – множество альтернатив.
. Каждому критерию ставится в соответствие нечёткое множество. Базовое множество – множество альтернатив.
 ;
; 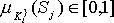 ;
; 


| S1 | S2 | … | Sm |
| S1 | ||||
| S2 | ||||
| … | ||||
| Sm |
Какой из двух альтернатив (Si, Sj) в большей степени принадлежит понятию  и насколько.
и насколько.
 ;
;  ;
;
Таким образом, решающее правило может быть сформулировано вербально следующим образом: лучшей считается та альтернатива, которая удовлетворяет критериям  и
и  ...
...  . Такое решающее правило может быть формализовано с помощью пересечений
. Такое решающее правило может быть формализовано с помощью пересечений  . Так как все эти критерии определены на одном и том же базовом множестве. В качестве лучшей альтернативы выбирается такая альтернатива которая имеет наибольшую степень принадлежности в K|.
. Так как все эти критерии определены на одном и том же базовом множестве. В качестве лучшей альтернативы выбирается такая альтернатива которая имеет наибольшую степень принадлежности в K|.
Если критерии различной важности, то оценивают эту важность  ;
;  .
.
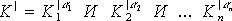 ;
;  ;
;  ;
; 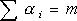 .
.
Решающее правило задано вербально с помощью следующих правил:
<обобщённая цель> = (<цель>/<цель>
op <цель>))
<цель> = (<”элементарная цель”>/<цель>
op <цель>)).


Обобщённая цель – дерево;
Листья – элементарные цели;
Ветвления – H.
Методы построения функции принадлежности нечётких множеств.Применение теории нечётких множеств для практики задаётся в качестве первого шага предполагаемой формализации нечётких понятий. В основании теории всегда лежит основание для построения понятия (например, механика – точка, квантовой теории – понятие состояний). Для теории нечётких множеств таким понятием является функция принадлежности.
Классификация методов построения:

Необходимо поставить в соответствие определённую степень принадлежности.
Эти значения согласуются с его предпочтениями:
- x1 x2 Î X
 ;
; - x1 x2 Î X
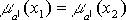 ; x1 и x2 – не различные относительные понятия A.
; x1 и x2 – не различные относительные понятия A.
Такое соотношение задаётся в виде графика или аналитического выражения с параметрами.
|

| Уровни совместимости между значениями оценки x и значениями ЛПР | Численные значения | Лингвистические оценки | Комментарии | |
| A | полная | очень хорошо | ядро нечётких множеств | |
| B | большая | 0.75 | хорошо | |
| C | средняя | 0.5 | достаточно хорошо | |
| D | малая | 0.25 | посредственно | |
| E | не совместимая | очень плохо | значения, которые располагаются вне носителя |
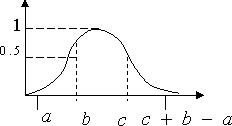
Стандартный набор графиков.
ЛПР выбирает подходящий график, а затем в диалоге выясняет и контролирует параметры.
|
|

Дата добавления: 2015-04-18; просмотров: 366; Мы поможем в написании вашей работы!; Нарушение авторских прав |

