Выбор альтернатив на основе композиционного правила вывода.

Рассматривается метод, многокритериального выбора альтернатив с использованием композиционного правила вывода и ограничения описаний альтернатив с информацией о предположениях ЛПР, заданных в виде нечётких суждений “если”, “то”.

1. Формируем множество критериев и множество альтернатив, ставим в соответствие каждому критерию лингвистическую переменную (имя, T_i, S, G_i, m_i) = K_i, где ; .

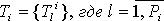Все критерии задаются на базовом множестве S: альтернативы {S_j}, где | {K_i}, .

2. Предпочтения ЛПР выражены правилами если-то, причём онтецеденты содержат составные выражения, состоящие из базовых термов лингвистических критериев, соединённых связками “и”, “или” и модификациями “не”, “очень”, “более-менее”. Консеквент представляет собой значение лингвистической переменной, которая указывает на то, как составное выражение удовлетворяет цели ЛПР:

<”степень соответствия с целью”, T, [0,1], G, M>

Рассмотрим пример:

T* = T È G(T) = {“удовлетворительное”, “более чем удовлетворительное”, “безупречное”, “очень удовлетворительное”, “неудовлетворительное”}

;

В общем виде: d_i: если , то ; i = 1,r.

3. Так как K_i задаются на базовом множестве S, то после выполнения È, Ç и модификаторов, получим: d_i: если то . Далее формализуем его в виде нечёткого отношения , .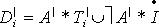

4. При выводе будут учитываться правила , тогда . Можно учесть важность каждого правила u_I = r*n_I, тогда .

5. Степень соответствия S_j определим с помощью композиционного правила вывода: , где - степень соответствия с обобщённой целью;

6. Сравнение нечётких множеств, заданных на единичном интервале, и на основании этого ранжировать альтернативы.