Решение квадратного неравенства

Неравенство вида

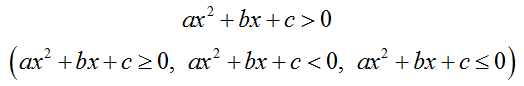
где x - переменная, a, b, c - числа, , называется квадратным.

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения . Для этого необходимо найти дискриминант данного квадратного уравнения. Можно получить 3 случая: 1) D=0, квадратное уравнение имеет один корень; 2) D>0 квадратное уравнение имеет два корня; 3)D<0 квадратное уравнение не имеет корней.

В зависимости от полученных корней и знака коэффициента a возможно одно из шести расположений графика функции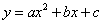

Если требуется найти числовой промежуток, на котором квадратный трехчлен 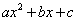больше нуля, то это числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если требуется найти числовой промежуток, на котором квадратный трехчлен 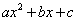меньше нуля, то это числовой промежуток, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое - не входят.

Такой метод решения квадратного неравенства называется графическим.

Решение квадратных неравенств методом интервалов.

Пример 1.

1. Рассмотрим функцию .

2. Найдем нули этой функции, решив уравнение:

корня

;

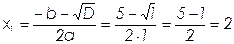3. Отметим полученные значения на числовой оси:

а)

б) Получили три промежутка:

1. Определяем знаки, которые принимает функция на каждом их этих промежутков:

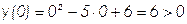
5. Выделяем те промежутки, которые удовлетворяют искомому неравенству:

1. Записываем ответ: .