МНК в случае линейной модели

Пусть регрессионная зависимость является линейной:

Пусть y — вектор-столбец наблюдений объясняемой переменной, а — это -матрица наблюдений факторов (строки матрицы — векторы значений факторов в данном наблюдении, по столбцам — вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

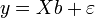
Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров и приравняв производные к нулю, получим систему уравнений (в матричной форме):

.

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

где все суммы берутся по всем допустимым значениям .

Если в модель включена константа (как обычно), то 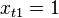при всех , поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений , а в остальных элементах первой строки и первого столбца — просто суммы значений переменных: и первый элемент правой части системы — .

Решение этой системы уравнений и дает общую формулу МНК-оценок для линейной модели:

Для аналитических целей оказывается полезным последнее представление этой формулы (в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические). Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая — вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на СКО (то есть в конечном итогестандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор — вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство МНК-оценок для моделей с константой — линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что МНК-оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является МНК-оценкой — удовлетворяет критерию минимума суммы квадратов отклонений от неё.

[править]Простейшие частные случаи

В случае парной линейной регрессии , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

Отсюда несложно найти оценки коэффициентов:

Несмотря на то что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа 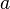должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид ; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели . В этом случае вместо системы уравнений имеем единственное уравнение

Следовательно, формула оценки единственного коэффициента имеет вид