Количественная оценка информации. Формула Хартли, формула Шеннона.

Основная задача Т.И. – создание систем связи, обеспечивающих заданную точность при минимальных значениях следующих параметров систем: мощность, полоса частот, время передачи и т.п. Отсюда вытекают 2 технические проблемы: 1.изыскание способов передачи больших объемов инф-и при малых ресурсных, временных, материальных затратах. 2. повышение достоверности принятой инф-и. При повышении достоверности принятой инф-и скорость передачи инф-и уменьшается, а стоимость технич. средств увеличивается. Т.о., возникает необходимость количественного определения инф-и, которая может передаваться по каналам связи с заданной достоверностью. [Количество инф-и, которое несет в себе сообщение, возрастает при увеличении кол-а неопределенности относительно того, какое сообщение из всех возможных будет выбрано. 1 из 10 возможных сообщений несет в себе меньшее кол-во инф-и, чем 1 из 1000000.]

В виде единицы информации принято использовать бит.

Мера информации – то, что может измерить информацию.

Бит – кол-во инф-ии, кот. необходимо, чтобы сообщить, что было выбрано одно из двух равновероятных событий. (Двоичный код – 1 или 0). Если кол-во бит =1, то I=1*log 2=1 бит.

Пример равновероятных событий – подбрасывание монетки.

Алфавит из 2х элементов: m=2 (кол-во символов алфавита).

Передается один элемент: n=1 (кол-во элементов сообщения).

Число различных сообщений: N; N=m^n

Заслуга Хартли в том, что он впервые предложил логарифмическую меру количества информации.

I=log (N)=log (mⁿ)

Log зависит от того, в чем мы будем измерять информацию (в битах – двоичный log).

Если символы неравновероятны, то мы не можем использовать эти формулы. Шеннон предложил формулу с учетом вероятностей характеристик. Формула Шеннона для неравновероятных символов: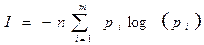

(- , так как вероятность (0,1)) где p_i- вероятность выбора символа s. Она учитывает вероятность появления каждого символа. След-но, p_i будет меньше нуля, а кол-во инф-ии не может быть отрицательным)

В случае равновероятных символов она переходит в формулу Хартли

Доп.вопрос:

Может ли инф-ия быть меньше 1 бита?

Теоретически инф-ия м.б. < 1 бит (0-вер-ть одного события, 1 – вер-ть другого). Инф-я = 1бит для равновероятностных ответов, в ост. случаях она меньше 1 бита.

Как это связано с основной задачей теории информации? Для чего это надо?

Нужно измерять задачу количественно. Измерение кол-ва инф-ии – частная задача. Решение частных задач приводит к решению общих задач.