Основной этап.

Шаг 1. Если bk-ak < l, то остановиться; точка минимума принадлежит интервалу [ak,bk]. В противном если F(pk)>F(qk), то перейти к шагу 2, а если F(pk)<=F(qk),то к шагу 3.
Шаг2. Положить a[k+1]=pk, b[k+1]=bk, p[k+1]=qk, q[k+1]=a[k+1]+0.618(b[k+1]-a[k+1]). Вычислить F(q[k+1]) и перейти к шагу 4.
Шаг3. Положить a[k+1]=ak, b[k+1]=qk,q[k+1]=pk, p[k+1]=a[k+1]+(1-0.618)(b[k+1]-a[k+1]). Вычислить F(p[k+1]) и перейти к шагу 4. Шаг4. Заменить k на k+1 и перейти к шагу 1.

Указать хотя бы один недостаток прямых методов – слабая сходимость.

в) Методы, использующие производные функции.

Достоинства – методы этого класса обладают высокой скоростью сходимости вблизи точки оптимума.

Условия применения – функция должна быть выпуклой.

Представитель: метод касательных (метод Ньютона).

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть — определённая на отрезке идифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где α — угол наклона касательной в точке .

Следовательно, искомое выражение для имеет вид:

Итерационный процесс начинается с некоего начального приближения x₀ (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).

г) Методы оптимизации многомодальных функций.

Достоинства – можно применять и для мультимодальных функций.

Представитель: метод ломанных. Этот прямой метод рассчитан на минимизацию мультимодальных функций, удовлетворяющих условию Липшица. В нем используются кусочно-линейные аппроксимации функции , графиками которых являются ломаные.

Условие применения этого метода – функция должна удовлетворять условию Липшица.

Задача безусловной оптимизации функций многих переменных

Постановка задачи

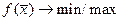
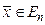, х –вектор из n-мерного пространства (принадлежит всему Эвклидову пространству) без ограничений.

Методы решения

а) Классический метод

Недостатки аналогичны недостаткам классического метода оптимизации функции одной переменной.