Интерполирование алгебраическими многочленами

Пусть на отрезке заданы точки (будем называть их узлами интерполирования), в которых известны значения функции . Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени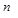

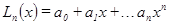, (1)

значения которого в заданных точках совпадают со значениями функции в этих точках.

Для любой непрерывной функции сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов 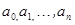получаем систему линейных уравнений

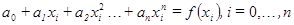(2)

Если среди нет совпадающих, то определитель системы (1.2) отличен от нуля, и следовательно система имеет единственное решение.

Определение Многочлен , удовлетворяющий условию

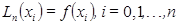(3)

называется интерполяционным многочленом для функции , построенным по узлам .

Решение системы (1.2) можно записать различным образом. Наиболее употребительна запись интерполяционного многочлена в форме Лагранжа и в форме Ньютона.

Интерполяционный многочлен Лагранжа имеет вид

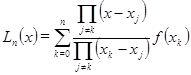(4)

Интерполяционная формула Ньютона позволяет выразить интерполяционный многочлен через значения в одном из узлов и через разделенные разности функции , построенные по узлам .

Интерполяционным многочленом Ньютона называется многочлен

, (5)

где - разделенные разности.

Интерполяционную формулу Ньютона удобнее применять в том случае, когда интерполируется одна и та же функция , но число узлов интерполирования увеличивается. Если узлы интерполяции фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться формулой Лагранжа.

(Дополнительно!) Разделенные разности

Пусть имеется табулированная функция . Введем понятие разделенной разности.

Разделенные разности нулевого порядка совпадают со значениями самой функции.

Разделенные разности второго порядка

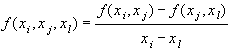и т.д.

Разделенные разности - го порядка :

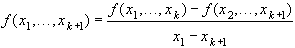(14)